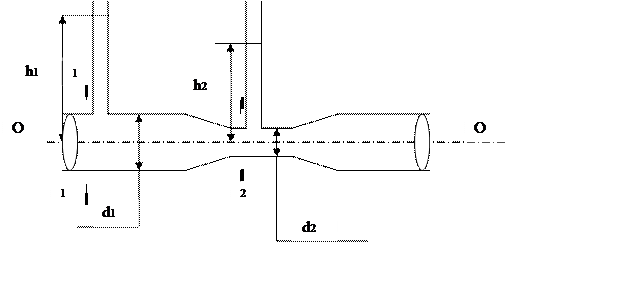
 |
|
Сечение (1;1): Z1 = 0; Р1/j –пьезометрическая высота, поэтому Р1/j = h1; V1 – скорость движения жидкости в сечении (1; 1),
можно определить для нашего случая по формуле: V1 = Q/S1, где S1 – площадь живого сечения трубопровода в
сечении (1; 1), определяется по формуле: S1 = π d1²/4. Величина α1 – коэффициент Кориолиса, 
учитывающий неравномерность распределения
скоростей, при турбулентном режиме движения жидкости ≈ 1,поэтому в нашем случае
его можно не брать в расчёт.
Сечение (2;2): Z2 = 0; P2/j – пьезометрическая высота = h2; V2 – скорость движения жидкости в сечении (2; 2), определяется по формуле: V2 = Q/S2, где S2 – площадь живого сечения, S2 = π d2²/4, коэффициент Кориолиса α2 ≈ 1,можно также не учитывать при расчётах.
Теперь подставляем определённые величины в уравнение Бернулли:
h1 + V1²/2g = h2 + V2²/2g, отсюда h2 = h1 + V1²/2g - V2²/2g = h1 + 1/2g · (V1²- V2²).
Для определения h2 осталось только определить величины V1 и V2. их находим по ранее записанным формулам, но предварительно переводим известные величины расхода в [м³/с], а диаметров в [м]:
Q = 3л/с = 0,003 м³/с; d1 = 75мм =0,075м; d2 = 40мм = 0.04м
V1 = 0,003 · 4/3,14 · 0,075² = 0,679м/с
V2 = 0,003 · 4/3,14 · 0,04 ² = 2,388м/с
Следовательно, h2 = 0,8 + 1/19,6 · (0,679 ² + 2,388 ²) = 0,53м.
Ответ: Вода в пьезометрической трубке подсоединённой к суженному сечению водопроводной трубы при данном расходе поднимется на 0,53м.
2.2 Задача 21 в-9
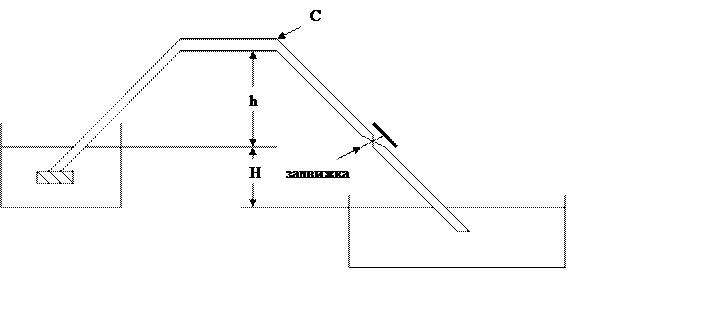
Из одного резервуара в другой вода поступает по сифонному трубопроводу длинной L и диаметром d. Определить расход воды Q при разности уровней в резервуарах H. Трубопровод снабжён приёмным клапаном с сеткой и задвижкой. Потерями напора в коленах и на выходе из трубы пренебречь. Коэффициент сопротивления трения λ = 0,03.
Найти вакуум в опасной точке сифона, если длина участка трубопровода до этой точки L1 и её возвышение над уровнем воды в верхнем резервуаре h.
Исходные данные: L = 40м; d = 100мм; H
= 7м; L1 = 25м; h = 3м; ξкл = 5; ξзад = 4.
 |
Решение:
Определить расход воды Q можно по формуле Q = V · S, где V- средняя скорость движения жидкости, а S – площадь живого сечения трубопровода, определяется по формуле: S = π · d2/4. Отсюда расход воды Q = V · π · d2/4.
Для определения средней скорости движения жидкости воспользуемся уравнением Бернулли для потока реальной жидкости:
Z1 + Р1/j + α1V1²/2g = Z2 + P2/j + α2V2²/2g + ∑hw
Выберем плоскость сравнения совпадающей с уровнем жидкости в нижнем резервуаре и обозначим (О; О). Первое сечение трубопровода возьмём совпадающим с уровнем жидкости в верхнем резервуаре и обозначим (1;1). Второе сечение трубопровода возьмём совпадающим с плоскостью сравнения и обозначим (2;2).
 |
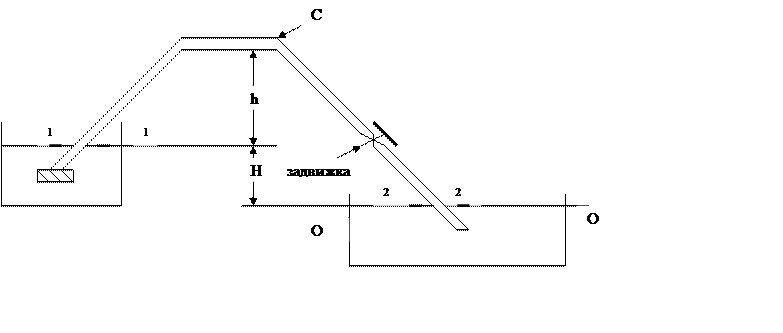Проанализируем величины в сечениях: сечение (1;1): Z1 = H; Р1 = Ратм; V1 = V2 = V поскольку диаметр трубопровода неизменный; α1 ≈ 1, поскольку режим движения жидкости турбулентный.
Сечение (2;2): Z2 = 0; Р2 = ρg · (H + h); α2 ≈ 1; ∑hw – суммарные потери напора складываются из потерь напора по длине и потерь напора связанных с местными сопротивлениями: ∑hw = hl + Σhм, где hl = λ · L/d · V2/2g, а Σhм = ξкл V2/2g + ξзад V2/2g.
Следовательно: ∑hw = V2/2g ∙ (λ · L/d + ξкл + ξзад)
Найденные величины подставляем в уравнение Бернулли:
H + Ратм/j + α1V²/2g = ρg · (H + h)/j + α2V²/2g + V2/2g ∙ (1 + λ · L/d + ξкл + ξзад), поскольку α1 = α2 , а j = ρg, то после нескольких сокращений уравнение приобретает вид:
Ратм/j = h + V2/2g ∙ (1 + λ · L/d + ξкл + ξзад), отсюда найдем скорость:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.