Определение манометрического давления в верхней части одного из сообщающихся сосудов, наполненных водой, под действием силы, приложенной к поршню правого сосуда, страница 3

V = √(Р_атм/j – h) · 2g / (1 + λ · L/d + ξ_кл + ξ_зад) , подставим в полученную формулу исходные данные, для этого переведём все параметры в систему СИ: Р_атм = 101323Па; d = 0,1 м; V = √(101323/9800 – 3) · 19,6/(1 + 0,03 · 40/0,1 + 5 + 4) = 2,56м/с.

Дальше находим расход по ранее записанной формуле: Q = 2,56 · 3,14 · 0.01/4 = 0,0201м³/с или Q = 20,1 л/с

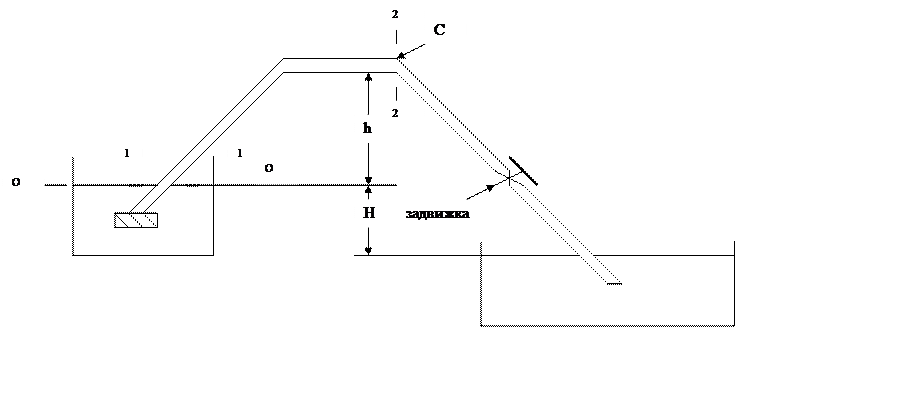
Чтобы решить вторую часть задачи возьмём плоскость сравнения совпадающей с уровнем жидкости в верхнем резервуаре, обозначим (0;0). Первое сечение возьмём также на плоскости сравнения, обозначим (1;1). Второе сечение возьмём у опасной точки сифона (С), обозначим (2;2).

Проанализируем величины из уравнения Бернулли для реальной жидкости в сечениях по очереди:

Сечение (1;1): Z₁ = 0; Р₁ = Р_атм; V₁ = V₂ = V; α₁ = α₂  ≈ 1 – режим движения жидкости турбулентный.

Сечение (2;2): Z₂ = h; Р₂ = Р_вак; ∑h_w = h_l + Σh_м.

Где h_l = λ · L₁/d · V²/2g, а Σh_м = ξ_кл V²/2g

Подставим определенные величины в уравнение Бернулли и получим уравнение вида:

Р_атм /j = h + Р_вак /j + V²/2g ∙ (1 + λ · L₁/d + ξ_кл), в полученном уравнении все величины известны, но Р_вак не является абсолютным давлением. Найдем абсолютное давление: Р_вак = Р_атм - Р₂^абс , следовательно, Р₂^абс = Р_атм - Р_вак. Подставляем найденную величину в полученное уравнение:

Р_атм /j = h + (Р_атм - Р_вак) /j + V²/2g ∙ (1 + λ · L₁/d + ξ_кл), раскроем скобки (Р_атм - Р_вак) /j и перенесём Р_вак /j в левую сторону уравнения, а Р_атм /j в правую, получим уравнение вида:

Р_вак /j =  h + V²/2g ∙ (1 + λ · L₁/d + ξ_кл), здесь Р_вак /j = h_вак – вакуумметрической высоте, значит, уравнение можно записать так:

h_вак = h + V²/2g ∙ (1 + λ · L₁/d + ξ_кл), подставим в него исходные данные:

h_вак = 3 + 2,56²/19,6 ∙ (1 + 0,03 ∙ 25/0,1 + 5) = 7,5м.

Отсюда Р_вак  = 7,5 ∙ 9800 =73500Па

Ответ: при заданных разностях уровней, параметрах трубопровода, местных сопротивления расход воды будет составлять 20,1л/с, а вакуумметрическое давление в опасной точке сифона 73,5 ∙ 10³ Па или 0,75 кг/см².

2.3. Задача 23 в-9:

Определить максимально допустимую высоту установки насоса h над уровнем воды в бассейне при следующих данных: Производительность насоса Q = 30л/с; допустимый вакуум во всасывающем патрубке Р_вак = 0,65кг/см²; длина всасывающей трубы L = 10м; её диаметр d = 200мм. Всасывающая труба снабжена приёмным клапаном с сеткой (ξ_кл = 6) и имеет одно сварное колено (ξ_кол = 1,2). Коэффициент сопротивления трения определить по эквивалентной шероховатости ∆ = 0,2мм, предполагая наличие квадратичной зоны сопротивления.

Решение:

Для определения допустимой высоты установки насоса нужно воспользоваться уравнением Бернулли для реальной жидкости: Z1 + Р1/j + α1V1²/2g = Z2 + P2/j + α2V2²/2g + ∑h_w. Выбираем плоскость сравнения совпадающей с уровнем жидкости в бассейне, обозначаем (0;0). Первое сечение возьмём на плоскости сравнения, обозначим (1;1). Второе сечение возьмём непосредственно на входе трубопровода в насос, обозначим (2;2).

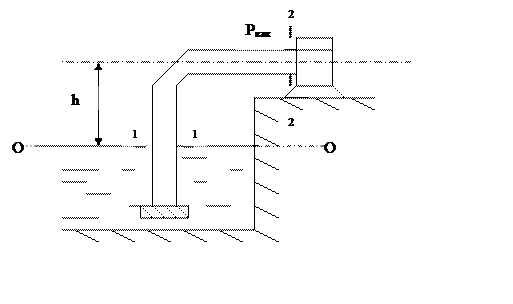
Проанализируем величины из уравнения Бернулли в сечениях: сечение (1;1):

Z₁ = 0; Р₁ = Р_атм; V₁ = 0. Сечение (2;2): Z₂ = h; Р₂ = Р_вак ; V₂ = Q/S, где S = π ∙ d²/4; α ≈ 1, поскольку режим движения жидкости турбулентный. Суммарные потери напора:

∑h_w = h_l + Σh_м, где h_l = λ · L/d · V²/2g; Σh_м = ξ_кл V²/2g + ξ_кол V²/2g, следовательно, полные потери напора определяются по формуле:

∑h_w = V²/2g ∙ (λ · L/d + ξ_кл + ξ_кол). Значение коэффициента λ найдём по графику Мурина, определив относительную гладкость, зона сопротивления – квадратичная. Относительная гладкость – d/∆ = 200/0,2 = 1000, отсюда λ из графика = 0,020. Найденные величины подставим в уравнение Бернулли: