Ратм /j = h + Рвак / j + V2/2g ∙ (1 + λ · L/d + ξкл + ξкол), для дальнейших действий необходимо привести значения давлений к одному виду и единицы измерений к системе СИ:
Рвак = Ратм + Р2абс , отсюда Р2абс = Ратм - Рвак; Ратм = 760мм рт ст. = 101323 Па
Рвак = 0,65кг/см2 = 63765 Па; Q = 30л/с = 0,03м3/с, далее уравнение приобретает следующий вид:
Ратм / j = h + (Ратм - Рвак) / j + V2 / 2g ∙ (1 + λ · L/d + ξкл + ξкол), отсюда выразим высоту: h = Рвак / j - V2/2g ∙ (1 + λ · L/d + ξкл + ξкол), осталось найти значение V и подставить исходные данные в полученную формулу.
V = 4 ∙ 0,03/ 3,14 ∙ 0,22 = 0,955м/с
Следовательно: h = 63765/9800 – 0,9552/19,6 ∙ (1 + 0,02 ∙ 10/ 0,2 + 6 + 1,2) ≈ 6,1м
Ответ: при заданных параметрах насоса и трубопровода насос необходимо устанавливать не выше 6,1метра над уровнем жидкости в бассейне.
2.4. Задача Д6 в-17.
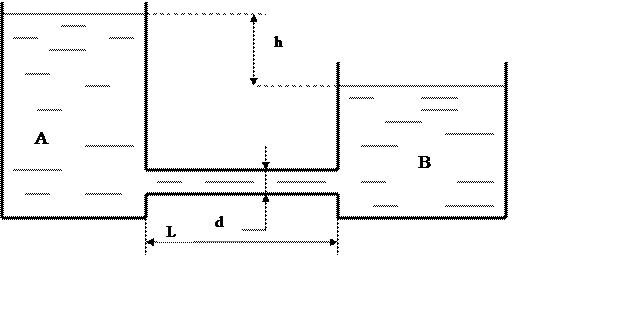
Нефть перетекает из резервуара А в резервуар В по трубе длиной L, диаметром d и с шероховатостью ∆. Найти и начертить графически зависимость расхода Q от разности уровней h при 0 ≤ h ≤ hмах. Скоростью движения нефти в резервуарах пренебречь. Кинематическая вязкость ν = 0,30см2/с.
Исходные данные: L = 30м; d =150мм; ∆ = 0,25мм; hмах = 5,5м.
![]()
Решение:
Для определения зависимости Q от h необходимо сначала найти зависимость V от h, поскольку Q = V ∙ S, где V – средняя скорость движения жидкости, в данном случае нефти, а S – площадь живого сечения трубопровода, определяется по формуле:
S = πd2/4, где d – диаметр трубопровода в [м]
Среднюю скорость движения нефти определим из уравнения Бернулли для реальной жидкости:
Z1 + Р1/j + α1V1²/2g = Z2 + P2/j + α2V2²/2g + ∑hw
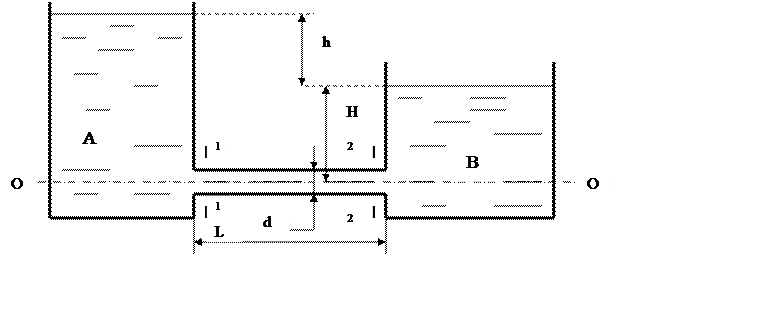
Возьмём плоскость сравнения совпадающей с осью симметрии трубопровода, обозначим (0;0). Первое сечение возьмём на выходе трубопровода из резервуара А, обозначим (1;1). Второе сечение возьмём на входе трубопровода в резервуар В, обозначим (2;2). Высоту от уровня жидкости в резервуаре В до плоскости сравнения обозначим буквой H. Сравним величины из уравнения Бернулли в сечениях по очереди, примем режим движения жидкости турбулентным.
Сечение (1;1): Z1 = H + h; Р1 = ρg ∙ (H + h), так как атмосферное давление действует на нефть в обоих резервуарах, то при расчётах его не берём; V1 = V2 = V; α1 = α2 = 1.
Сечение (2;2): Z2 = H; Р2 = ρg ∙ H; суммарные потери напора в данном случае рассчитываются по формуле: ∑hw = hl; поскольку местные потери напора не учитываются. Потери напора по длине определяются так: hl = λ · L/d · V2/2g, так как принят режим движения – турбулентный.
 |
Подставив, определённые в сечениях величины, в уравнение Бернулли получим:
H + h + ρg ∙ (H + h)/j + αV²/2g = Н + ρg ∙ H/j + αV²/2g + λ · L/d · V2/2g, после ряда сокращений одинаковых величин, в ходе переноса их из одной части уравнения в другую, а также с учётом того что j = ρg, получим уравнение вида: 2h = λ · L/d · V2/2g.
Из этого уравнения выразим среднюю скорость движения жидкости:
V = √4g∙h·d ∕ λ·L, коэффициент λ найдём из графика Мурина, определив относительную гладкость - d ∕∆ = 150 ∕0,25 = 600, следовательно λ = 0.022.
Подставим заданные величины в формулу средней скорости движения жидкости:
V = √4 ∙ 9,8 ∙ h ∙ 0,15 ∕0,022 ∙ 30 = √8,91 ∙ h = 2,98 ∙ √h.
Теперь значения средней скорости движения жидкости и площади живого сечения подставим в формулу определения объёмного напора:Q=V ∙S.
Q = 2,98 ∙ √h ∙ 3,14 ∙ 0,152/4 = 0,05 ∙ √h.
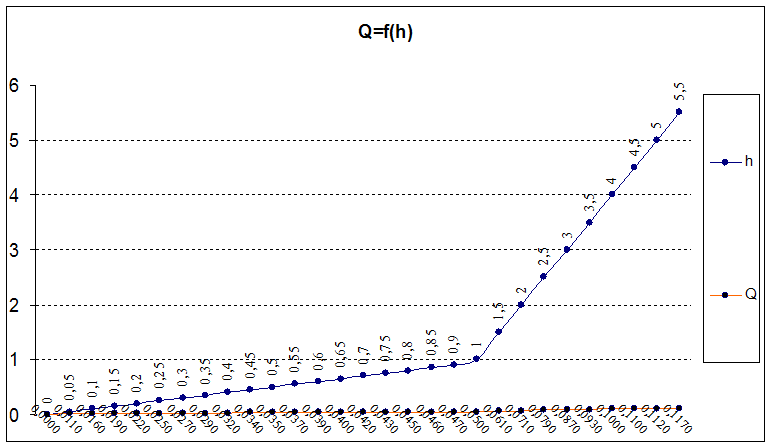
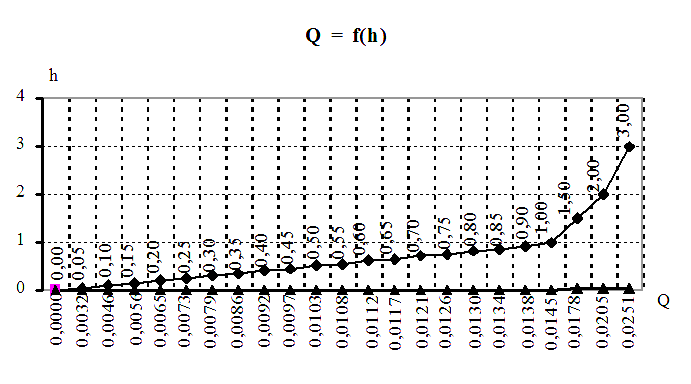
Строим график зависимости Q
= 0,05 ∙ √h, где Q [м3/с], а h [м]. 
Список используемой литературы:
1. Конспект лекций.
2. П. Е. Осипов. „Гидравлика. Гидравлические машины и гидропривод”.
3. А. В. Андреевская, Н. Н. Кременецкий, М. В. Панова „Задачник по гидравлике”.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.