Статистический метод оценки количества информации. Оптимальное планирование перевозок

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Магнитогорский государственный технический университет им. Г. И. Носова»

Кафедра промышленного транспорта

Отчет по выполнению лабораторных работ

по дисциплине «Информатика (спецкурс)»

Вариант №17

Выполнил: студент Журкин А.Ю.

Группа ГТ-10(1)

Институт ГТиТ

Проверил:                                     

Магнитогорск 2010

Содержание

Лабораторная работа №1. 2

Лабораторная работа № 2. 7

Лабораторная работа №1

«Статистический метод оценки количества информации»

Цель работы: экспериментальная проверка зависимости количества информации в сообщении о случайном событии от вероятности осуществления этого события.

Таблица 1- Исходные данные для выполнения лабораторной работы

№ вар.	закон	параметры	закон	параметры
17	Бета	А=400; В=2000;  α=7; β=8;	Равномерный	—

где A – минимальное значение заданного интервала, B – максимальное значение заданного интервала, αи β- параметры распределения.

Вероятность моделируемых событий описывается различными законами распределения случайной величины (СВ). Полученный в результате моделирования ряд чисел – значений вероятности событий используется для расчета количества информации (в битах) в сообщении об этом событии.

Для расчета необходимо использовать формулу К. Шеннона

        ,                                              (1)

где — вероятность -го исхода события из N возможных исходов.

Ход выполнения лабораторной работы:

Этап 1. Запустить на выполнение программу Excel.

На чистом «листе» электронной таблицы в ячейку A1 ввести формулу, результатом которой будет значение СВ. Для генерации равномерно-распределенной на заданном интервале значений СВ рекомендуется использовать функцию Randbetween(A;B), где A – минимальное значение заданного интервала, B – максимальное значение заданного интервала.

Этап 2. На практике случайные процессы (транспортные, в частности) описываются законами распределения СВ, отличными от равномерного.

Для первой СВ задано бета-распределение. Для данного закона распределения рекомендуется пользоваться функцией БЕТАРАСП(Х; α; β; A; B;), где Х- значение СВ  в интервале между А и В, α и β- параметры распределения, A и B – соответственно нижняя и верхняя границы изменения X.

Для второй СВ задано равномерное распределение, для которого рекомендуется использовать формулу СЛЧИС().

Этап 3. В качестве СВ в формулах используются значения столбца «А» электронной таблицы.

Количество информации (в битах), содержащейся в сообщении о случайном событии, имеющем вероятность P, рассчитывается по формуле Шеннона

H = -SXlog2X,                                                        (2)

где Х- случайная величина.

График зависимости количества информации в сообщении о случайном событии от вероятности осуществления этого события представлен на рисунке 1

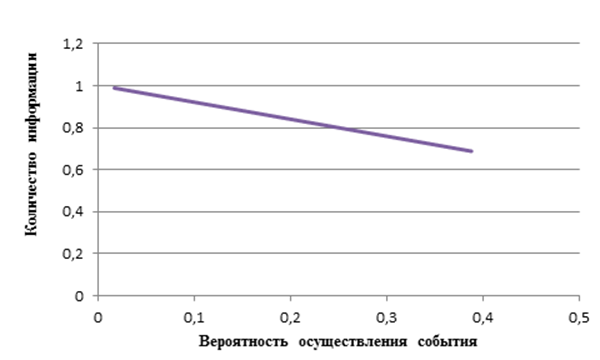
Рисунок 1

Этап 4. Для анализа полученных результатов и выявления зависимости необходимо рассчитать частоту передачи сообщений с различным количеством информации и по результатам расчетов построить график (рис. 2). Для этого значения количества информации необходимо сгруппировать по N интервалам.

Количество интервалов группировки N рекомендуется принимать равным от 10 до 12.

Тогда величина интервала (шаг) определиться как

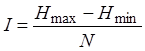,                                                              (3)

где  и  - соответственно максимальное и минимальное значение количества информации в сообщении (для определения этих значений рекомендуется воспользоваться функциями Excel МАКС(ряд_чисел) и МИН(ряд_чисел), где «ряд_чисел» – расчетный ряд, содержащий 500 значений).

Для нахождения интервалов необходимо использовать формулу:

r_i=r_i-1+I,                                                                      (4)

где r_i-искомый интервал, r_i-1-предыдущий интервал, I-величина интервала.

Для подсчета частот необходимо использовать следующую формулу:               =ЧАСТОТА(массив данных; массив интервалов),                              (5)

где «массив данных» -данные столбца «количество информации в битах», а «массив интервалов» - вычисленные интервалы.

Вычисленные практические данные представлены в таблице 2.

Таблица 2- Практические данные

закон	максимум	минимум	количество информации (H)	закон	максимум	минимум	количество информации (H)
Бета	-4503,71	-6190227	1528936095	Равномерный	356,5055	0,50285	-91582,3

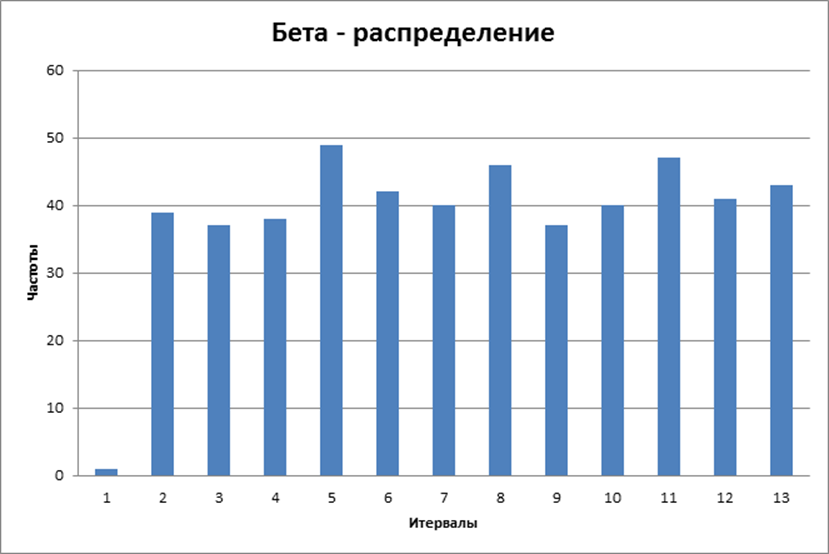
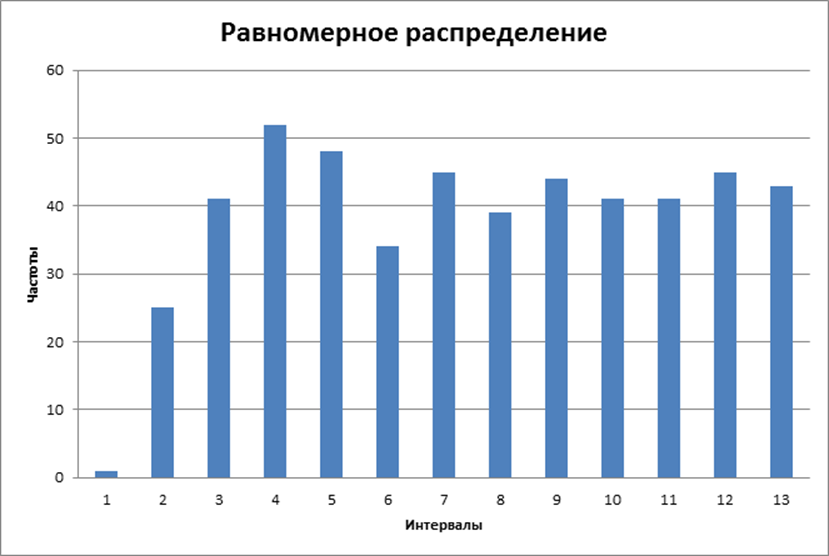
Рисунок 2