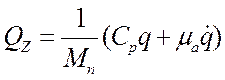Плавность хода колесных машин. Дифференциальное уравнение колебаний автомобиля, страница 6

                                                                                      (24)

Как найти и ?

Если профиль дороги синусоидальный, то получим

                                  q = q_osinpt                                                                         (25)

где P - круговая частота колебаний;

t  - время;

q_o- амплитуда длины неровности.

Тогда первая производная от q, по времени будет равна

                                                                                                           (26)

Подставив выражения (25) и (26) в выражение (24), получим

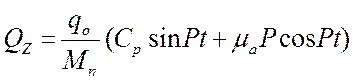                                                                (27)

Или после преобразований получим

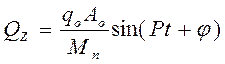                                                                                    (28)

где     - введенное обозначение;

φ - начальная фаза колебаний - смещение по фазе.

Введем другое обозначение – коэффициент

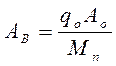
Окончательно дифференциальное уравнение вынужденных колебаний будет иметь вид

                                                           (29)

Решение такого линейного неоднородного дифференциального уравнения дается в справочнике по высшей математике.

Решение будет иметь вид

                                                                                     (30)

где  Z_o - начальная амплитуда вынужденных колебаний; 

δ  - начальная фаза колебаний подрессоренной массы.

Здесь

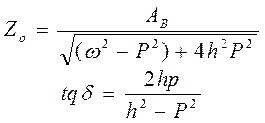
где  h_р - коэффициент затухания.

Другие производные перемещения получают перемножением на частоту возмущения

Ż = ZP      (30);                              и                                     (31)

Непосредственно по уравнениям амплитуд выявить влияние основных дорожных условий на параметры плавности хода, а также сравнить воздействие конструктивных факторов у разных автомобилей затруднительно.

Поэтому более наглядное представление об этом могут дать амплитудно-частотные характеристики.

Амплитудно-частотной характеристикой называется графическая зависимость между частотой вынужденных колебаний (при данной длине волны она пропорциональна скорости движения автомобиля V) с одной стороны и амплитудами колебаний (Z_max   и φ_max) и ускорениями корпуса ( и ) с другой.

Таким образом, для построения амплитудно-частотных характеристик нам необходимо знать: максимальные амплитуды колебаний и ускорения в зависимости от скорости движения автомобиля, высоты и длины неровности.

Эти величины могут быть определены расчетом или экспериментально.

При расчетном определении параметры подсчитывают по формулам, задавшись высотой неровности h  и длиной волны l.

Амплитудно-частотная характеристика имеет вид, приведенный на рис. 7.

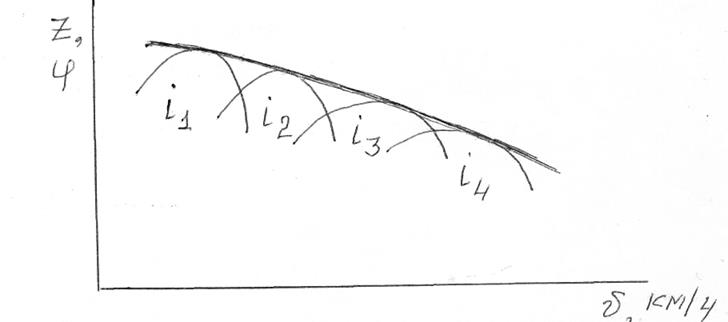
Рис. 7. Амплитудно-частотная характеристика

ЗАКЛЮЧЕНИЕ

Таким образом, в одной лекции в обобщенном и сконцентрированном виде мы рассмотрели основные вопросы плавности хода автомобиля: виды колебаний автомобиля, параметры оценки плавности хода, а также выводом получили дифференциальные уравнения свободных и вынужденных колебаний автомобиля. Мы также ознакомились с характеристиками различных типов упругих элементов.

Рассмотренные вопросы являются ключевыми вопросами плавности хода автомобиля и позволяют понимать процессы, происходящие в подвеске автомобиля при его движении.

 

 

 

НАЧАЛЬНИК КАФЕДРЫ № 8

доцент, кандидат технических наук

полковник                      Ю.МИХАЛЕВ