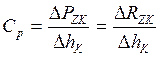Плавность хода колесных машин. Дифференциальное уравнение колебаний автомобиля, страница 4

                                                                                                   (1)

Иногда жесткостью C_p называют производную от нагрузки ∆Р_ZК по перемещению ∆ h_k.

У подвески с линейной характеристикой жесткость постоянная и выражается графически как тангенс угла наклона характеристики (рис. I, д)

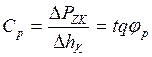                                                                                                    (2)

Для торсиона (рис. I, в)

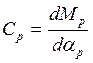
где dMp - приращение момента, приложенного к торсиону;

dα_p – приращение угла закрутки торсиона.

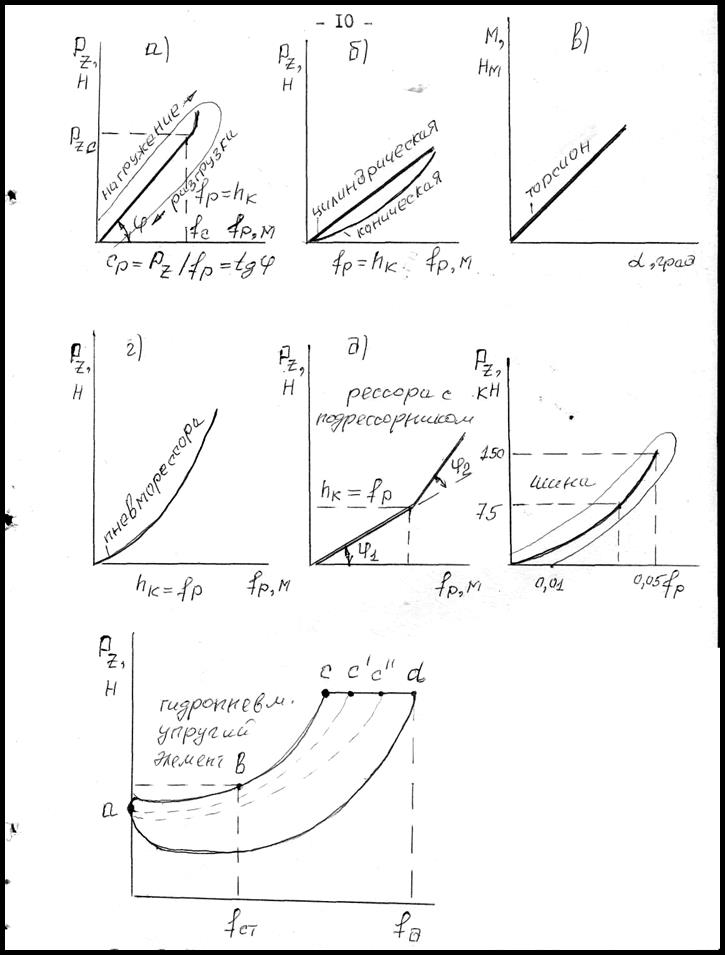
ab - сжатие воздуха в полости А; bc – сжатие жидкости (резкое возрастание сопротивления); с – отключение гидравлического элемента и далее сжимается только воздух;  bc′ или bc″ - жидкость перетекает только через калибр отверстия; da – обратный ход (роль амортизатора).

Рис. 1. Характеристика упругих элементов подвески:

а - листовой рессоры; б – цилиндрической и конической пружины; в – торсиона; г – пневморессоры; д – рессоры с подрессорником; е – шины;

ж – гидропневматического упругого элемента 

 

2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ АВТОМОБИЛЯ

Расчетную схему одной из частей автомобиля можно представить так, как это показано на рис. 2.

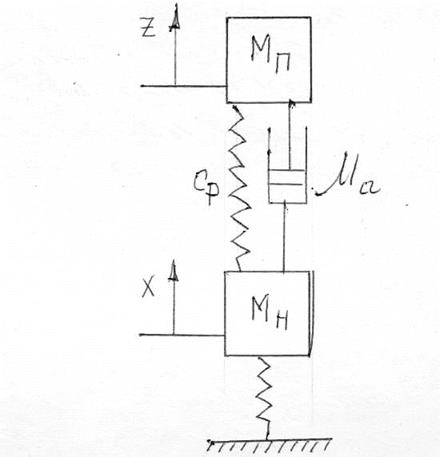
Рис. 2. Расчетная схема одной из частей автомобиля

M_п - масса подрессоренной части автомобиля (двигатель, груз, пассажиры и т.п.).

Это часть автомобиля, масса которой передается упругим элементам подвести.

М_н - неподрессоренная масса (элементы автомобиля, масса которых не передается на упругие элементы подвески);

X - перемещение неподрессоренной массы;

Z - перемещение подрессоренной массы.

Анализ колебаний этой расчетной схемы автомобиля можно производить на ее упрощенном варианте без учета влияния неподрессоренных масс. В таком случае расчетная схема автомобиля будет иметь вид, представленный на рис. 3.

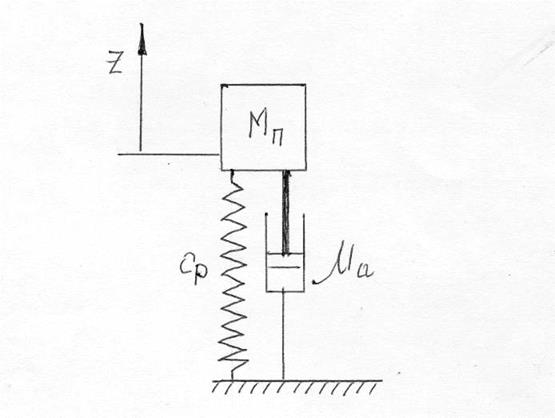
Рис. 3. Расчетная схема колебаний автомобиля

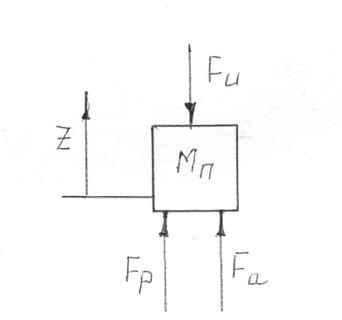
Рис. 4. Силы, действующие на подрессоренную массу автомобиля

Как видно из рис. 4 на подрессоренную массу автомобиля действуют следующие силы:

F_u - сила инерции;

F_p - сила упругости рессоры;

F_a - сила сопротивления амортизатора.

Уравнение равновесия для рис. 1 будет иметь вид

                            F_u + F_p + F_a = 0                                                                         (4)

Координата Z отсчитывается от статического равновесия. Сила инерции может быть определена по формуле

                                                                                                       (5)

где   - вторая производная от вертикальных перемещений (ускорения).

                                       F_p = C_pZ                                                                         (6)

где Ср - жесткость рессоры (упругого элемента);

Z  - перемещение.

                                    F_a = μ_aŻ                                                                             (7)

где μ_а - коэффициент сопротивления амортизатора;

Ż - первая производная от вертикальных перемещений (скорость перемещений).

Подставив выражения (5), (6) и (7) в уравнение (4), получим

                                                                           (8)

Разделив каждый член в уравнении (8) на М_п , получим

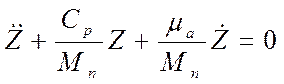                                                                             (9)

Введем следующие обозначения

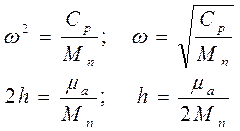
Здесь  ω - частота собственных колебаний;

h - коэффициент затухания колебаний.

Тогда дифференциальное уравнение собственных колебаний автомобиля будет иметь вид

                                                                                 (10)

Как известно из курса высшей математики, решение этого однородного дифференциального уравнения будет следующим

                                             Z=Ae^-ht sin(ωt + φ)                                            (11)

где А и φ _ произвольные постоянные, определяемые из начальных условий;

h - коэффициент затухания колебаний;

ω - частота собственных колебаний;

e = 2,718 (экспонента);