Плавность хода колесных машин. Дифференциальное уравнение колебаний автомобиля, страница 5

t - время.

Частота собственных колебаний может быть определена по формуле

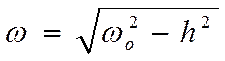                                                                                      (12)

где  ω_o - частота собственных колебаний без учета затухания.

Поскольку   , то можно считать, что ω ≡ ω_о, т.е. свободные колебания происходят с постоянной частотою, но с амплитудой, убывающей по экспоненциональной зависимости (см. рис. 5)

Огибающая амплитуда будет иметь вид

                         А = ± А_ое^-ht                                                                                                      (13)

где  А_о - начальная амплитуда.

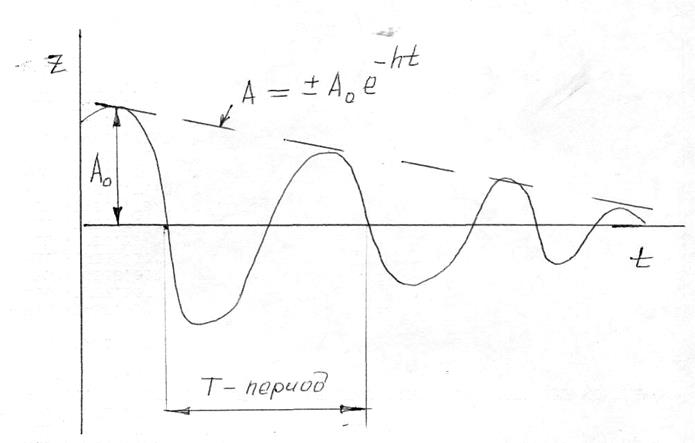
Рис. 5. Затухание свободных колебаний

Мы получили выражение для определения частоты собственных колебаний

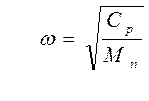                                                                                              (14)

из которого следует, что она зависит от жесткости упругого элемента (С_р) и подрессоренной массы автомобиля. Следовательно, собственная частота колебаний зависит от загрузки автомобиля.

Из формулы для определения коэффициента затухания

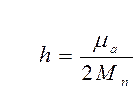                                                                                               (15)

также следует, что h  зависит от коэффициента сопротивления амортизатора (μ_а) и подрессоренной массы автомобиля (М_п ).

Опыт разработки и эксплуатации автомобилей показывает, что оптимальная величина ω лежит в пределах 10-11,5 рад/с, а  h в пределах 1,15...2 рад/с.

Эффективность затухания колебаний может быть оценена так на-зеваемым декрементом затухания

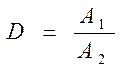                                                                                                   (16)

который показывает во сколько раз уменьшается амплитуда А собственных колебаний за один период.

Чтобы учесть собственное влияние коэффициента затухания колебаний и жесткость подвески используют коэффициент апериодичности

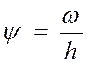                                                                                                           (17)

При ψ = 1 колебания будут апериодическими, т.е. затухнут в течение одного периода.

Практически ψ = 0,2...0,3.

3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ АВТОМОБИЛЯ

При движений автомобиля по чередующимся неровностям возникают вынужденные колебания, частота которых определяется характером возмущающей функции, а параметры - сложной зависимостью внешних условий и конструктивных факторов.

Для составления дифференциального уравнения вынужденных колебаний воспользуемся методом Даламбера, согласно которому сумма всех сил, действующих на подрессоренную массу, равна нулю.

Для решения этой задачи, как и в предыдущем случае, составим расчетную схему колебаний автомобиля (рис. 6)

На подрессоренную массу действуют силы:

F₁ - сила упругости рессоры;

F₂ - сипа сопротивления амортизатора;

F₃  - сила инерции подрессоренной массы.

Определим силу упругости рессоры

                                  F₁ = C_p (Z –q)                                                                   (18)

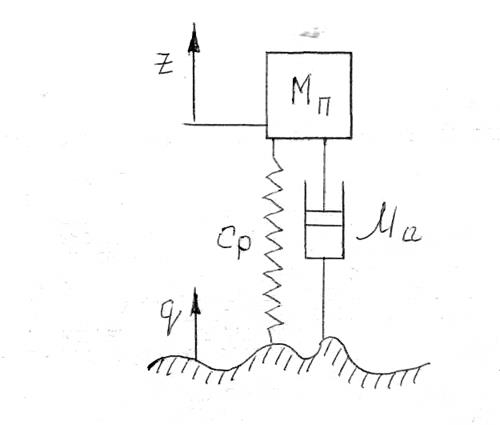
Рис. 6. Расчетная схема автомобиля где  С_p- жесткость рессоры;

Z - перемещение подрессоренной массы;

q - высота неровности.

Сила сопротивления амортизатора

                                                                                                                 (19)

Сила инерции подрессоренной массы

                                                                                                     (20)

Уравнение равновесия будет иметь вид

                                    F₁ + F₂ + F₃ = 0                                                             (21)

Подставив в уравнение (21) выражения (18), (19) и (20), получим

Или после преобразований получим

                                                   (22)

Поделив левую и правую части уравнения (22) на М_п, получим

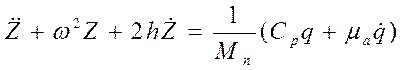                                                       (23)

Это и есть дифференциальное уравнение вынужденных колебаний автомобиля.

Правая часть этого дифференциального уравнения представляет собой возмущающую функцию