Ответы на 204 тестовых вопросов по разделам дисциплины "Теория автоматического управления" (Система автоматического управления. Недостатки магнитных усилителей), страница 4

91)  Изменение усилия на 20 Дб, соответствует изменению отношения двух амплитуд в 10 раз;

92)  Логарифмической фазовой частотной характеристикой (ЛФЧХ) называют  график зависимости фазовой частотной функции от логарифма частоты;

93)  В теории автоматического управления выделяют следующие типовые динамические звенья

безинерционное (пропорциональное), апериодическое (инерционное), дифференцирующее, интегрирующее, колебательное; запаздывающее;

94)  Безинерционным называют  звено, у которого выходная величина в каждый момент времени пропорциональна входной величине;

95)  Интегрирующим звеном называют  звено, в котором выходная величина пропорциональна интегралу во времени от входной величины;

96)  Колебательным звеном называют звено, у которого при ступенчатом изменении входной величины выходная величина стремится к новому установившемуся значению, совершая при этом колебания;

97)  Уравнение колебательного звена

98)  Уравнение безынерционного (пропорционального) звена

99)  Уравнение дифференцирующего звена

100) Уравнение апериодического звена

101) Назовите характеристики динамических звеньев верны все выше перечисленные ответы

Раздел 3

102) Под устойчивостью системы понимается  свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия;

103) Для какого процесса вводится понятие устойчивость? установившегося ;

104) Какое уравнение считается характеристическим? дифференциальный оператор при выходной величине приравненный к нулю;

105) Условие устойчивости линейной системы  для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения были правыми;

106) Расположение каких корней на комплексной плоскости является признаком устойчивости САУ?

P₅, P₆, P₇;

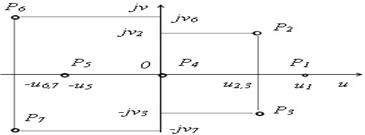107) Расположение каких корней на комплексной плоскости является признаком неустойчивости САУ? ) P₁, P₂, P₃

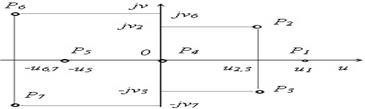108) Расположение каких корней на комплексной плоскости является признаком того, что САУ находится на границе устойчивости?  P₄

109) Чьи критерии устойчивости относятся к алгебраическим? Гурвица, Рауса; 

110) Характеристическое уравнение системы имеет вид:р² + 7р + 12 = 0. Определить, будет ли САУ в замкнутом состоянии устойчива?

признаком устойчивости системы второго порядка является положительность коэффициентов характеристического уравнения, следовательно, система устойчива;

111) Для уравнений какого порядка положительность коэффициентов является необходимым и достаточным признаком устойчивости? для уравнений первого и второго порядка;

112) Критерии устойчивости Рауса и Гурвица позволяет  по коэффициентам характеристического уравнения без вычисления его корней сделать суждение об устойчивости системы;

113) Сущность критерия устойчивости Гурвица  САУ устойчива, если все определители имеют знаки, одинаковые со знаками первого коэффициента характеристического уравнения, т.е. при a₀ > 0 были больше нуля;

114) Для САУ имеющей характеристическое уравнение четвертого порядка признаком устойчивости по критерию Гурвица является выполнения условия  a₀ > 0;  a₁ > 0; a₂ > 0;  a₃ > 0;  а₄>0; а₃(а₁а₂ – а₀а₃) – а₄ > 0;

115) Для САУ имеющей характеристическое уравнение третьего порядка признаком устойчивости по критерию Гурвица является выполнения условия a₀ > 0;  a₁ > 0;  a₂ > 0; a₃ > 0;    а₄>0; a₁a₂ – a₀a₃> 0;

116) Характеристическое уравнение имеет вид: 5р³ + 3р² +6р + 1 = 0, Используя критерий устойчивости Гурвица выберите правильный ответ.  все коэффициенты уравнения больше нуля, определитель второго порядка D₂=13>  0 следовательно, система устойчива

117) Используя критерий устойчивости Гурвица, определить устойчивость САУ, если её характеристическое уравнение имеет вид: 3р³ + 5р² + 4р + 6 = 0,где: а₀ = 3;     а₁ = 5;    а₂ = 4;     а₃ = 6.

Условие устойчивости: a₀ = 3 > 0;      a₁ = 5 > 0;      a₂ = 4 > 0;    a₃ = 6 > 0;D₂ > 0

Выразим определители Гурвица:

.

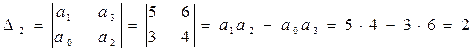Условие D₂ > 0 выполняется, следовательно, система устойчива.

118) Используя критерий устойчивости Гурвица, определить устойчивость САУ, если её характеристическое уравнение имеет вид: 5р³ + 2р² + 2р + 1 = 0,