Досліждення процесу випарювання гідроокису калію, аналіз його виробництва, страница 8

Рисунок 3.4 – Спільне зображення гарячої й холодної складових кривих

3.2 Каскадний метод

За допомогою каскадного методу можна без побудови графіків обчислювати цільові енергетичні значення.Для цього спочатку визначимо зрушені температурні інтервали з реальних температур постачання й цільових температур технологічних потоків процесу. Необхідно всі гарячі потоки зрушити по температурній осі вниз на DТ_min/2 (гаряча складова крива на DТ_min /2 холодніше, ніж у дійсності), а холодні потоки піднімемо на DТ_min /2 (холодна складова крива на DТ_min /2 гарячіше, ніж насправді).

Будуємо спеціальну таблицю 3.3, де записуємо реальні й зрушені температури.

Таблица 3.3 – Зрушені температури потоків

№ потоку	Тип потоку	G, кг/с	ТS,°С	ТT,°С	,°С	,°С
1	холодний	1,484	104,1	155,2	119,1	170,2
2	холодний	2,429	71,1	104,1	86,1	119,1
3	холодний	3,333	10	71,1	25	86,1
4	гарячий	1,3784	179,8	40	164,8	25
5	гарячий	1,1	130	40	115	25
6	гарячий	0,945	98,1	40	83,1	25
7	гарячий	0,384	155,2	55	140,2	40

Зрушені складові криві зараз стикаються в точці пінча. Холодна та гаряча температури пінча також змінилися на DТ_min /2, і зараз мають одне й теж значення. У результаті такого зрушення стає можлива теплопередача між потоками, що втримуються в гарячої й холодної складових кривих у межах кожного температурного інтервалу. Дуже важливо відзначити, що вертикальне переміщення кривих не змінює величини основних ентальпійних інтервалів.

Розташовуємо зрушені температурні інтервали й технологічні потоки уздовж температурної осі рис.3.5.

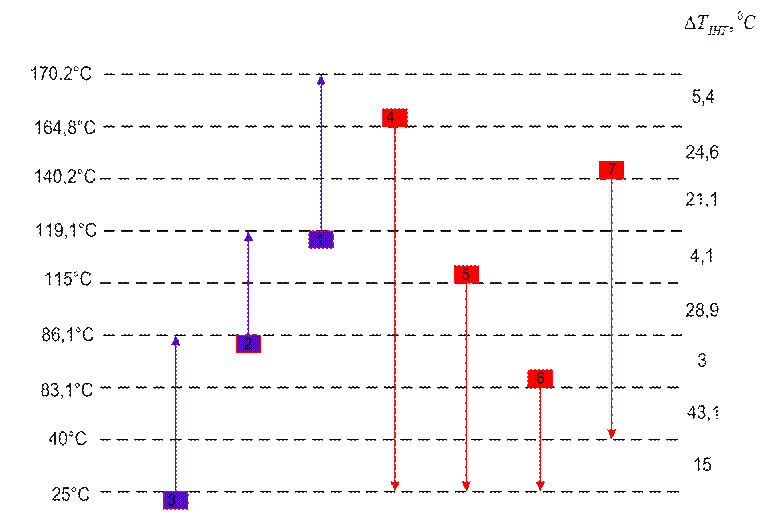
1, 2 и 3 – холодні потоки; а 4, 5, 6 и 7 – гарячі потоки

Рисунок 3.5 – Розташування зрушених температурних інтервалів та технологічних потоків уздовж температурної осі

Розраховуємо значення DТ для кожного інтервалу та ентальпійний баланс:

 

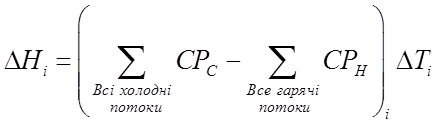                                                                                                       (3.17)

де DН_i – тепловий баланс для i-го зрушеного інтервалу, кВт;

DТ_i – величина i-го температурного інтервалу, °C;

СР_С та СР_Н – потокова теплоємність холодного та гарячих потоків, кВт/°С.

Розрахуємо DH для наступних інтервалів:

DH₁= СР₁ DТ₁=30,564 кВт

DH₂= CP₁ DТ₂ – СР₄·DТ₂ = 46,74 кВт

DH₃= (CP₁ – СР₇ − СР₄) DТ₃ = 18 кВт

DH₄= (CP₂ – СР₄ − СР₇) DТ₄ = 19,776 кВт

DH₅= (CP₂ – СР₄ − CP₇ – СР₅) DТ₅ = 18 кВт

DH₆= (CP₃ – CP₄ – СР₅ – СР₇) DТ₆ = 13,27 кВт

DН₇= (СР₃ – СР₄ – СР₅ – СР₆ – СР₇)= 29,134 кВт

DН₈= (СР₃ – СР₄ – СР₅ – СР₆)= 25,85 кВт

Отримані дані заносимо в таблицю 3.4.

Таблиця 3.4 – Тепловий баланс у температурних інтервалах

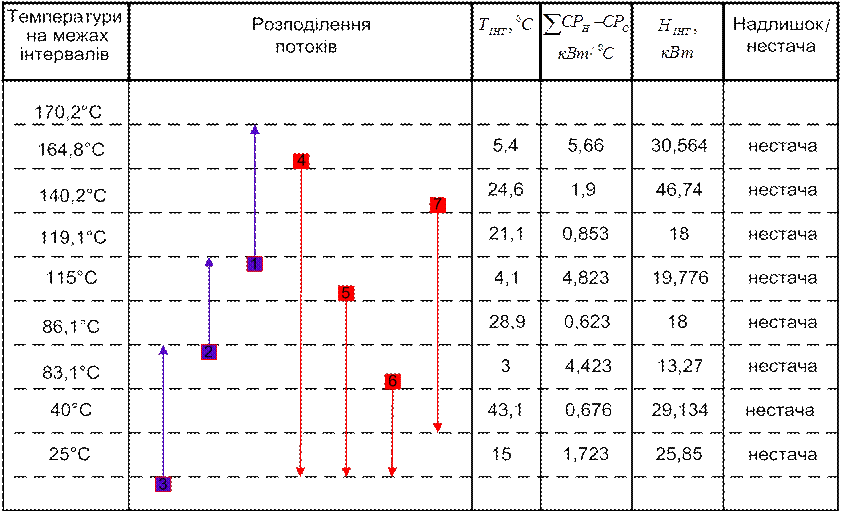
Розташуємо наші температурні інтервали уздовж температурної шкали, спадаючим донизу каскадом. Спочатку припустимо, що перший температурний інтервал не одержує теплової енергії від зовнішніх енергоджерел (рис. 3.6.).

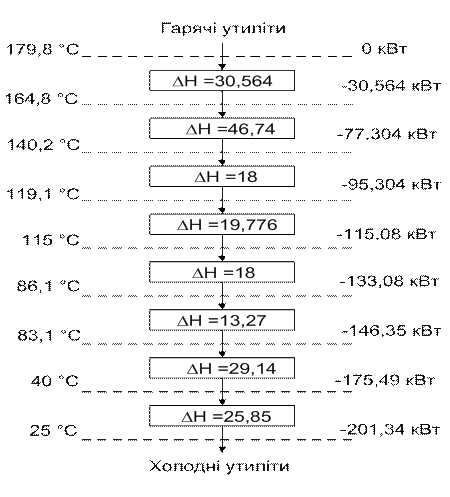
ΔН – Тепловий баланс теплового інтервалу, кВт

Рис. 3.6 – Каскад табличного алгоритму при нульових гарячих утилітах

З рисунка 3.6 видно, що найбільше значення ΔН з мінусом буде при температурі 25 ºС. Це і буде точка пінча. Тому до першого температурного інтервалу підводимо максимальне значення ΔН = 201,34 кВт тепла, але з плюсом і таким чином розраховуємо увесь каскад, як показано на рисунку 3.7.

Побудуємо каскад позитивних теплових потоків. Для цього до гарячих утиліт додаємо 201,34 кВт і знаходимо тепловий баланс для кожного температурного інтервалу таким же чином, який наведено вище. У результаті одержали каскад табличного алгоритму при цільових значеннях гарячих утиліт [4].

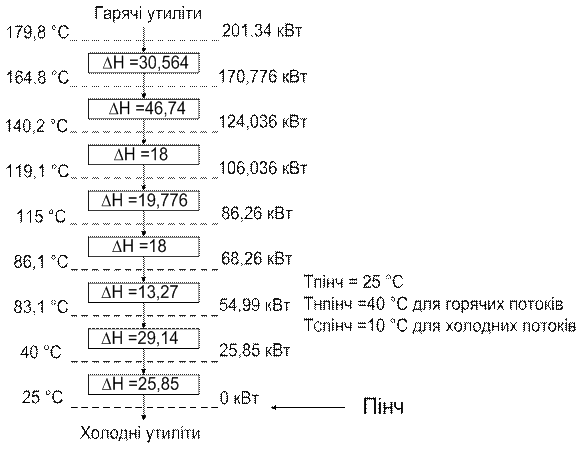
ΔН – Тепловий баланс теплового інтервалу, кВт