Z = 8.8258
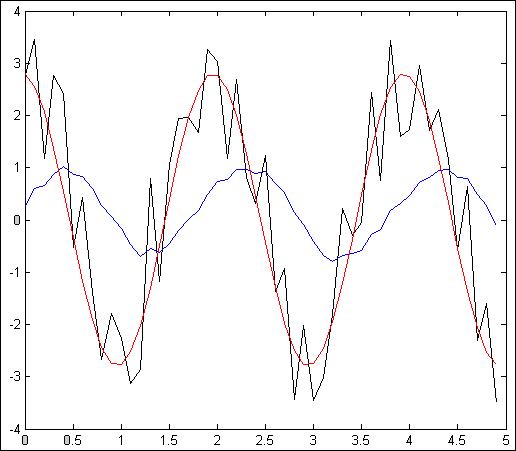
Рис.4.2.5. Зависимость при N =50, Т = 100мс, К=10
Z = 16.7688
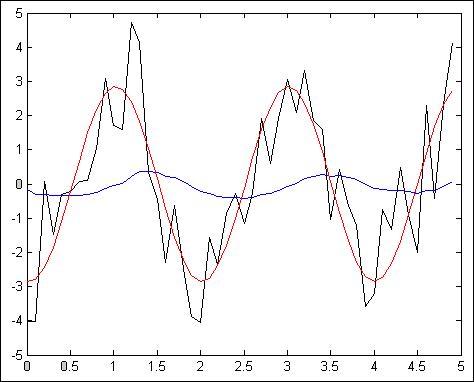
Рис.4.2.6. Зависимость при N =50, Т = 100мс, К=25
Z = 203.9231
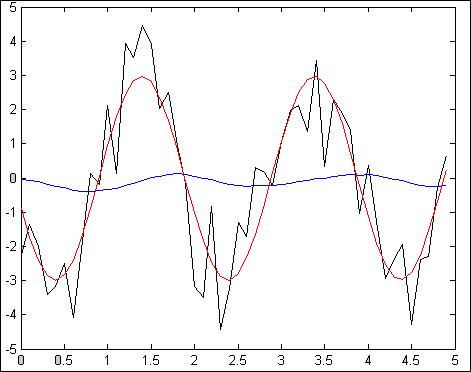
Рис.4.2.7. Зависимость при N =50, Т = 100мс, К=50
Z = 858.3716
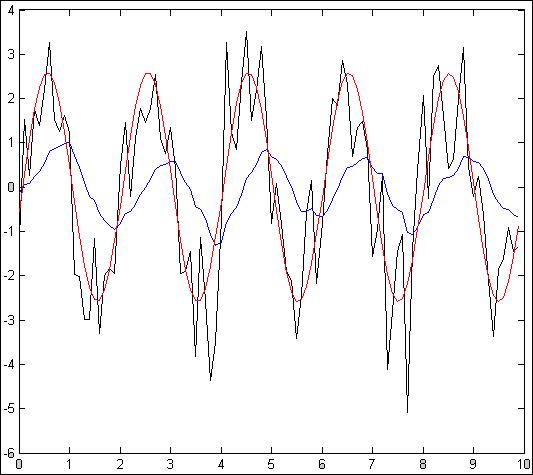
Рис.4.2.8. Зависимость при N =100, Т = 100мс, К=10
Z = 30.6289
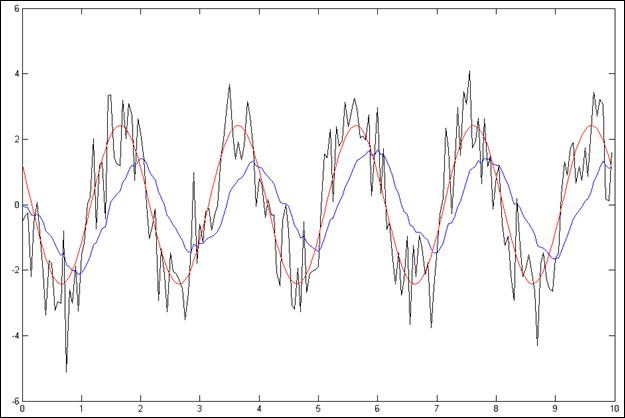
Рис.4.2.9. Зависимость при N =200, Т = 50мс, К=10
Z = 15.7013
Исходя из полученных зависимостей можно сделать следующие выводы:
- С увеличением коэффициента К(памяти фильтра) увеличивается запаздывание выходного сигнала, но уменьшается амплитуда (св-во интегратора)
- С увеличением периода дискретизации улучшается качество фильтрации(при соблюдении теоремы Котельникова, причем с избытком)
Запаздывание сигнала обусловлено памятью фильтра.
Данный фильтр является фильтром, реализующим обычный интегратор первого порядка, соответственно с улучшением качества фильтрации амплитуда резко падает(«интегратор» не успевает зарядиться, идет усреднение синусоиды). Также при выборе большего периода дискретизации фильтр интегрирует высокочастотную помеху типа «белый шум». Такой фильтр целесообразно использовать, если невозможно использовать обычный фильтр RC – например место на плате ограничено.
Исследования постоянного сигнала с помехами:
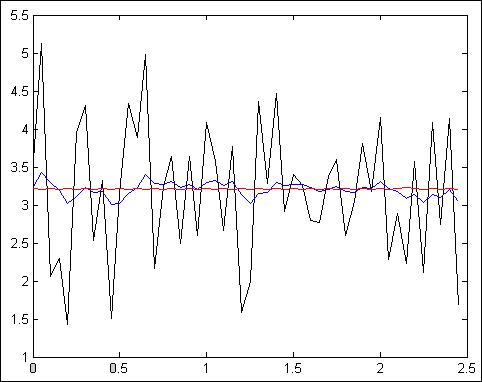
Рис.4.2.10. Зависимость при N =50, Т = 50мс, К=10
Z = 86.0043
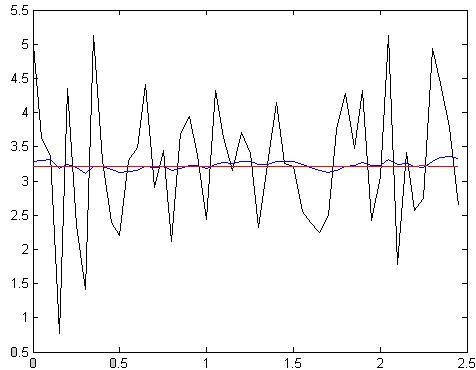
Рис.4.2.11. Зависимость при N =50, Т = 50мс, К=20
Z = 235.4892
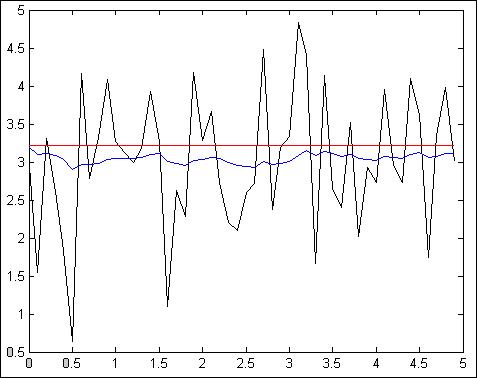
Рис.4.2.12. Зависимость при N =50, Т = 100мс, К=20
Z = 26.5018
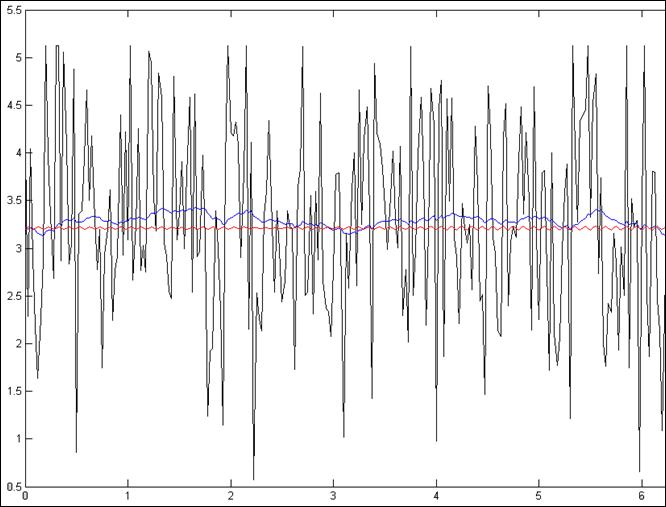
Рис.4.2.13. Зависимость при N =250, Т = 25мс, К=50
Z = 103.1884
Фильтрация постоянного сигнала алгоритмом усреднения с постоянным коэффициентом коррекции также показывает, что данный фильтр идентичен RC-цепочке: для наилучшей фильтрации постоянного сигнала необходимо уменьшить период дискретизации(иначе проинтегрируем постоянный сигнал и получим неверное значение), нужно увеличить коэффициент К, что обеспечит улучшение качества фильтрации – фильтр с большей памятью лучше фильтрует помехи и приближается к фильтру с бесконечной памятью.
4.3. Рекуррентный алгоритм усреднения с конечной памятью
Были исследованы возможности фильтрации как переменного во времени сигнала, так и постоянного.
Для полного исследования зависимостей изменялись параметры Т – времени дискретизации, объем выборки N и глубины буфера G.
Ниже приведены снятые характеристики,
Черный цвет – зашумленный сигнал на входе фильтра
Синий цвет – отфильтрованный сигнал
Красный цвет – полезный сигнал на входе.
Исследования синусоидального сигнала с помехами:
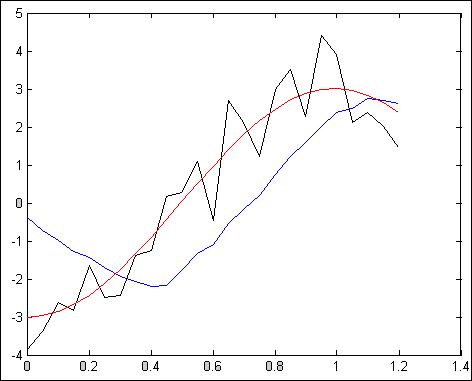
Рис.4.3.1. Зависимость при N =25, Т = 50мс, G=10
Z = 32.2193
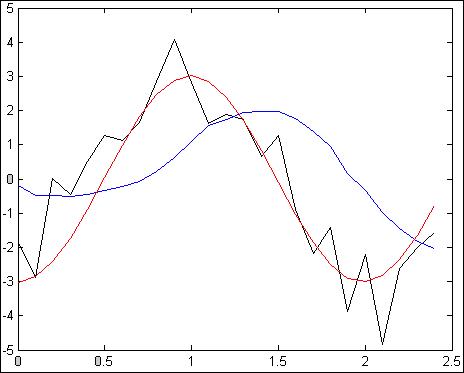
Рис.4.3.2. Зависимость при N =25, Т = 100мс, G=10
Z = 4.9047
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.