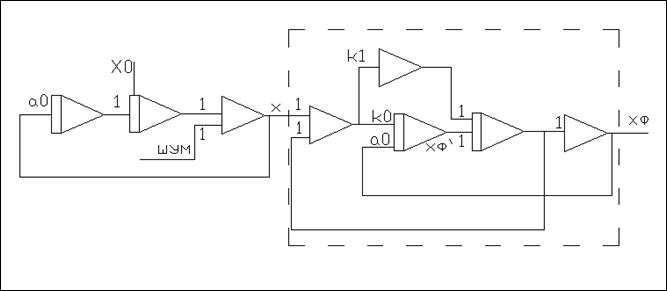
 Рис.3.1.3.
Схема эксперимента(фильтрация с применением модели объекта)
Рис.3.1.3.
Схема эксперимента(фильтрация с применением модели объекта)
4. Результаты эксперимента
4.1. Рекуррентный алгоритм усреднения с бесконечной памятью
Исследования проводились при заданном входном сигнале, равном 3.2 В.
Для полного исследования зависимостей изменялись параметры Т – времени дискретизации и объем выборки N.
Ниже приведены снятые характеристики,
Черный цвет – зашумленный сигнал на входе фильтра
Синий цвет – отфильтрованный сигнал.
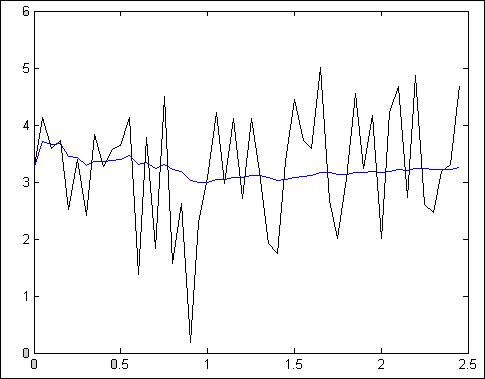
Рис.4.1.1. Зависимость при N = 25, Т = 50 мс
Z = 36.5103
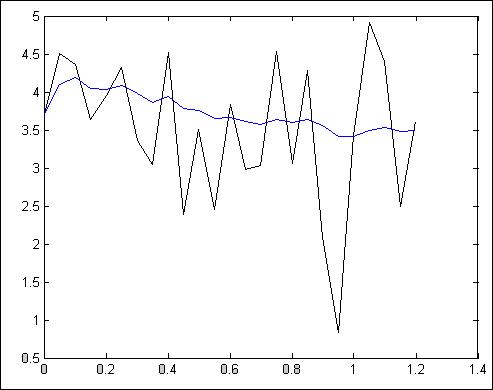
Рис.4.1.2. Зависимость при N = 50, Т = 50 мс
Z = 2.9480
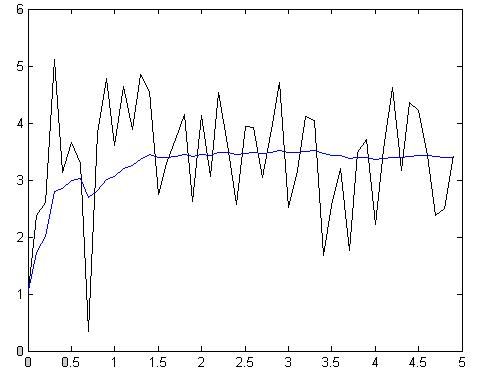
Рис.4.1.3. Зависимость при N = 50, Т = 100мс
Z = 4.5846
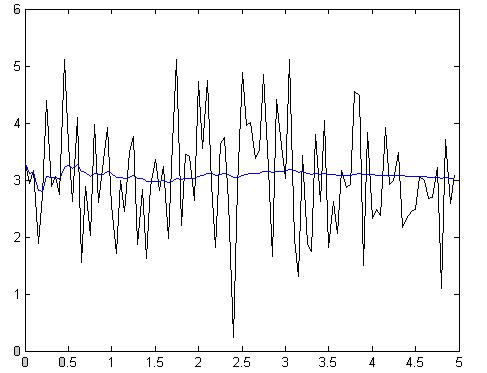
Рис.4.1.4. Зависимость при N =100, Т = 50мс
Z = 41.5521
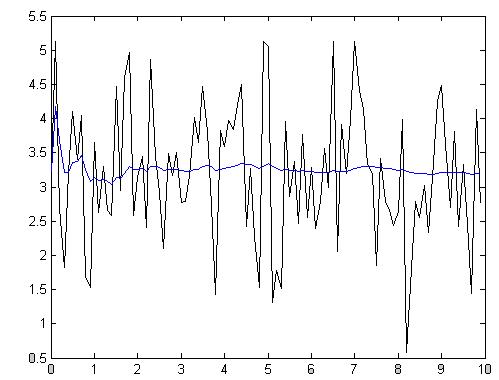
Рис.4.1.5. Зависимость при N =100, Т = 100мс
Z = 59.2815
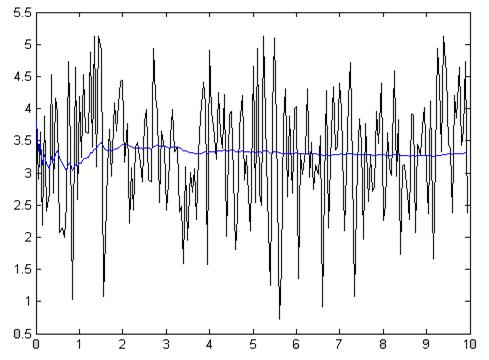
Рис.4.1.6. Зависимость при N =200, Т = 50мс
Z = 56.3056
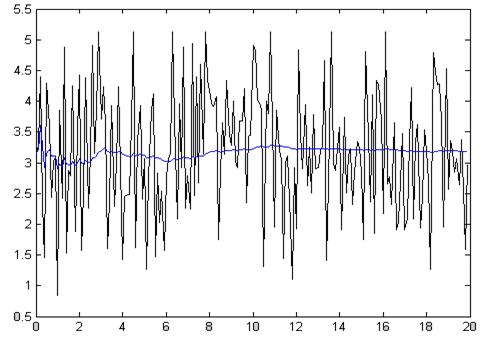
Рис.4.1.7. Зависимость при N =200, Т = 100мс
Z = 98.4680
Как видно из приведенных графиков и полученных коэффициентов Z, метод, основанный на усреднении работает тем лучше, чем выше объем выборки N. При этом в конечном значении выхода фильтра снижается доля, вносимая корректирующим членом, зависящим во многом от помехи, т.е. фильтр получает большую память. Полученные значения оценки эффективности Z дают представление о том, что метод работает тем точнее, чем больше наблюдаемое время, при этом объем выборки оставался постоянным – см. рис.4.1.4 - 4.1.5., 4.1.6. – 4.1.7.
Значения переменного во времени сигнала – синусоиды не приведены, поскольку данный фильтр не может обеспечить фильтрацию изменяющихся во времени сигналов даже теоретически. На практике получается некоторый переходный процесс, зависящий от точки начала работы фильтра, но при больших объемах выборки он сводится к усреднению синусоиды – к нулю.
4.2. Рекуррентный алгоритм усреднения с постоянным коэффициентом коррекции
Были исследованы возможности фильтрации как переменного во времени сигнала, так и постоянного.
Данный алгоритм реализует программно интегрирующее звено первого порядка.
Исследования синусоидального сигнала с помехами:
Для полного исследования зависимостей изменялись параметры Т – времени дискретизации, объем выборки N и коэффициента коррекции К.
Ниже приведены снятые характеристики,
Черный цвет – зашумленный сигнал на входе фильтра
Синий цвет – отфильтрованный сигнал
Красный цвет – полезный сигнал на входе.
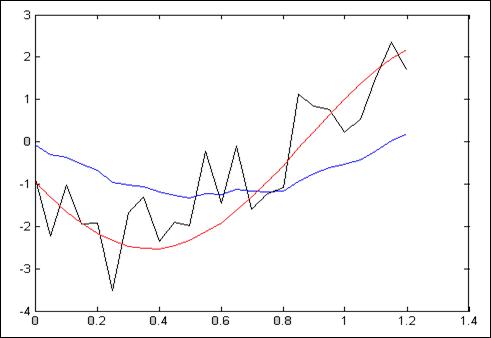
Рис.4.2.1. Зависимость при N =25, Т = 50мс, К=10
Z = 11.3486
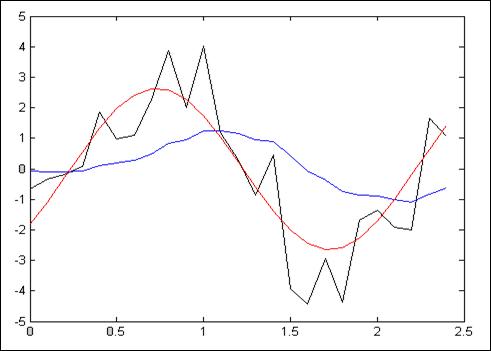
Рис.4.2.2. Зависимость при N =25, Т = 100мс, К=10
Z = 35.2196
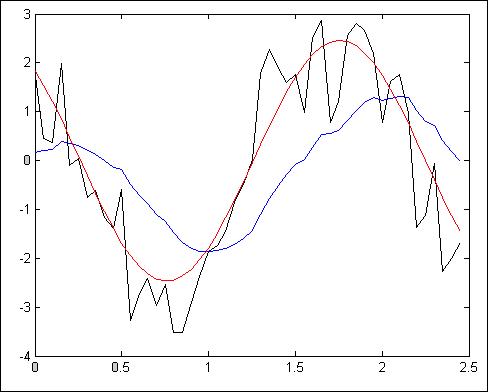
Рис.4.2.3. Зависимость при N =50, Т = 50мс, К=10
Z = 14.6362
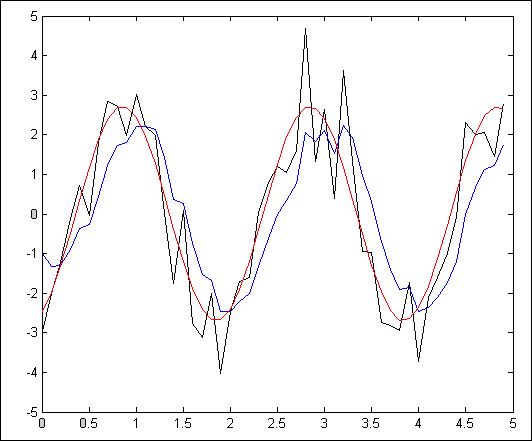
Рис.4.2.4. Зависимость при N =50, Т = 100мс, К=3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.