Статистический анализ плана формирования поездов

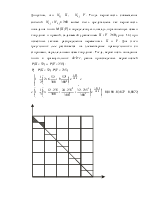
Задача 1.

Статистический анализ плана формирования поездов

Условие задачи: На заданном участке полигона сети железных дорог составить планы формирования поездов и провести их статистический анализ с использованием теории вероятности.

Исходные данные:

1. Вагоно-часы простоя под накоплением, cm                        А:   1500

                                                                                                  Б:   1300

                                                                                                  В:   1500

2. Экономия от проследования станции

без переработки, , ч                                                            Б:   1,5

                                                                                                  В:   5,0

3. Среднесуточные вагонопотоки в назначении  :                   АГ – 300

                                                                                                  АБ – 50

                                                                                                  АВ –

                                                                                                  БГ – 300

                                                                                                  БВ – 40

                                                                                                  ВГ – 30

4. Законы распределения: АГ – Э3(распределение Эрланга третьего порядка), БГ – Э4(распределение Эрланга  четвертого порядка)

Рис. 1.

          Решение.  Рассчитанный по средним значениям вагонопотоков план формирования реализуется для конкретных размеров потоков, имеющих в каждые данные сутки определенную вероятность отклонения от своих средних значений.

          При этом если отклонение превышает определенную величину, могут изменится и соответствия отдельных струй вагонопотоков сообразно условиям выделения их в самостоятельные назначения плана формирования поездов.

          Известным условием выделения струи вагонопотока в самостоятельное назначение является удовлетворение ее  неравенству:

,                                            (1.1)

где

 – мощность струи вагонопотока со станции i назначением на станцию j;

 –  экономия от проследования без переработки сортировочных станций, расположенных между станциями назначения данной струи и более ближней смежной струи ;

с –  параметр накопления вагонов в сортировочном парке на составы грузовых поездов;

m – среднее число вагонов в составе грузовых поездов.

          Выделение данной струи потока в самостоятельное назначение будет эффективно во всех случаях, когда

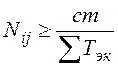.                                                (1.2)

Но в следствие колебаний потока мощность струи может уменьшиться до величины

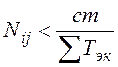,                                                (1.3)

При этом она перестанет удовлетворять необходимому и достаточному условиям выделения.

          Рассмотрим заданные в условии задачи функции распределения непрерывных величин.

          Большое число случайных величин в транспортных процессах описывается распределением Эрланга, в том числе, интервалы между поступлением поездов на станцию, длительность их расформирования и формирования и другие. Выражение плотности эрланговского распределения записывается в виде:

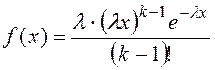,                                          (1.4)

где k – порядок распределения Эрланга;

 - интенсивность появления событий.

Математическое ожидание в эрланговском распределении рассчитывается по формуле:

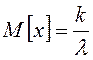.                                                    (1.5)

Функция распределения имеет вид:

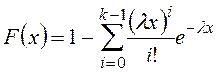.                                         (1.6)

В зависимости от величины k ,  по-разному выражается через элементарные  функции:

при  :   ,                                                                             (1.7)

при  :   ,                                                                 (1.8)

при  :  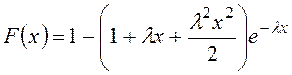 ,                                                    (1.9)

при  :  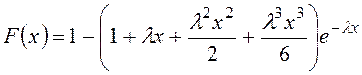  .                                     (1.10)

Если известно математическое ожидание , то согласно (1.5), формулы (1.7) – (1.10) можно записать, придавая численные значения коэффициенту k:

при  :  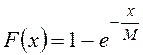 ,                                                                           (1.11)

при  :  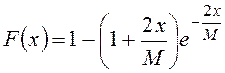 ,                                                             (1.12)

при  :  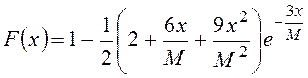 ,                                               (1.13)

при  :  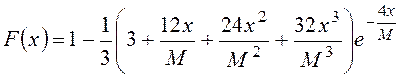  .                               (1.14)

При увеличении параметра кривые функции и плотности распределения становятся круче. При  кривые плотности распределения становятся приблизительно симметричными относительно математического ожидания, как и в случае нормального распределения.

          Случайные непрерывные величины могут иметь показательное распределение. Данное распределение является частным случаем распределения Эрланга (при ). Поэтому плотность и функция показательного распределения могут быть определены по формулам (1.4), (1.6) при  , а также (1.7) и (1.11).