Статистический анализ плана формирования поездов, страница 2

          Проанализируем план формирования поездов при заданных исходных данных.

1.  Пусть имеется полигон с четырьмя сортировочными станциями А, Б, В, Г и ступенчатый график вагонопотоков (рис. 1.2, а). На рисунке 1.2,б представлен оптимальный план формирования, рассчитанный по среднесуточным значениям, рассчитать который не представляет труда, так как струя  удовлетворяет необходимому  удовлетворяет достаточному условию, а остальные, даже будучи объединены, не удовлетворяют и необходимому. Величины  есть средние значения вагонопотоков.

2.  Рассмотрим теперь этот же полигон с учетом суточных колебаний вагонопотоков. Очевидно, что при заданных условиях достаточно располагать информацией о колебаниях двух струй потока   и .

3.  Суточные значения струи  распределены по закону Эрланга третьего порядка с параметрами вагонов. Суточные значения струи  распределены по по закону Эрланга четвертого порядка, а вагонов. Подсчитаем значения потоков, при которых происходит изменение соответствия их условиям выделения. Как видно, для струи  соответствие достаточному условию начинается с величины потока

.

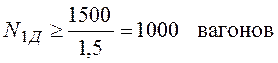Необходимому условию соответствует поток:

.

Для струи  необходимое и достаточное условия совпадают:

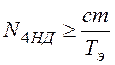.                                                 (1.15)

.

4.  Определим вероятности сохранения представленного на рис. 1.2,б варианта при изменениях потоков, а также вероятности сохранения других оптимальных планов формирования поездов.

а) Назначение АГ со струей будет, очевидно, эффективно для значений  от 230 вагонов и более. Вероятность этого события для распределения Эрланга третьего порядка можно определить по формуле

где  определяется по формуле (1.13) при условии, что .

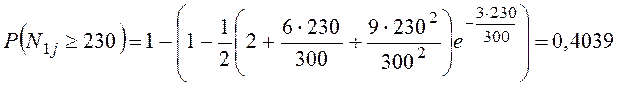
б) Вероятность появления суточных размеров струи вагонов, распределенной по закону Эрланга четвертого порядка, определим по формуле:

где  определяется по формуле (1.14) при условии, что .

                                  Рис.1.2.

Схема участка АГ, ступенчатый график вагонопотоков

и оптимальные варианты плана формирования поездов.

I вариант рассчитан по средним значениям ;

II вариант: при   вагонов в сутки и вагонов в сутки;

III вариант: при  вагонов в сутки и вагонов в сутки;

вариант: при  и , причем (нет ни одного сквозного назначения);

 вариант: при  и , причем .

.

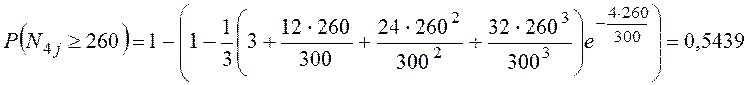в) Расчеты показывают, что по отдельности  выделение струй  и  в самостоятельные назначения эффективно в  дней для  и в  дней для . Однако в целом вероятность сохранения оптимального плана, показанного на рис. 1.2,б будет ниже и составит:

,

т.е.дней.

5. Рассмотрим случаи, когда вагонопотоки  и примут значения, меньше критических. Таких случаев может быть всего четыре:

1).   и  (соответствует рисунку 1.2,в) Вероятность такого случая можем рассчитать по формуле:

.

2).  и  (соответствует рисунку 1.2,г) Вероятность такого случая можем рассчитать по формуле:

.

3).  и . При этом , т.е. план формирования не имеет ни одного сквозного назначения (рисунок 1.2,д). Вероятность этого события может  быть подсчитана следующим образом.

Допустим, что ,  . Тогда вероятность совмещения событий  может быть представлена как вероятность попадания точки  в определенную площадь, ограниченную осями координат и прямой, задаваемой уравнением ( рис. 1.3) при известных законах распределения переменных  и . Доя этого треугольник оав разбивается на элементарные прямоугольники со сторонами, параллельными осям координат. Тогда, вероятность попадания точки в прямоугольник , равна произведению вероятностей  и :

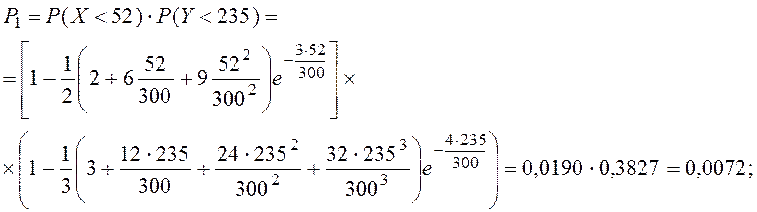
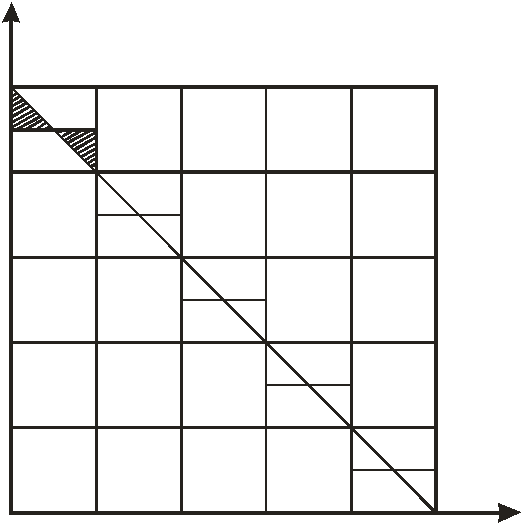
Рис.1.3

Вероятность попадания точки в следующий прямоугольник:

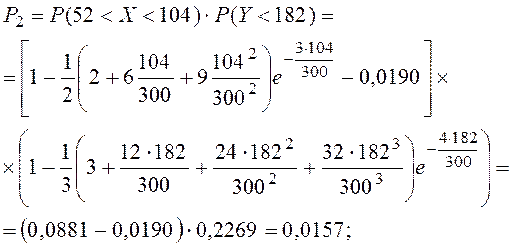
Аналогичным способом получаем:

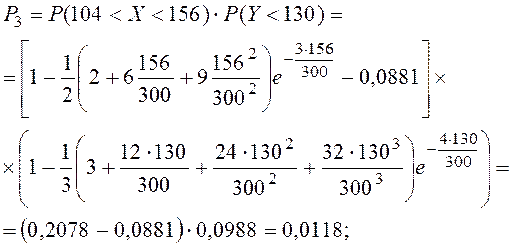
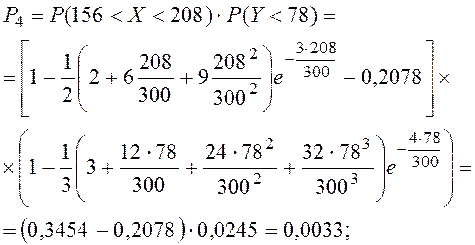
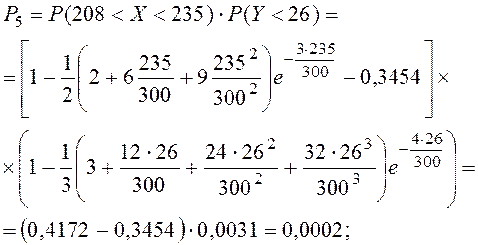
Суммарная вероятность попадания точки  в треугольник равна сумме вероятностей ее попадания в отдельные прямоугольники.

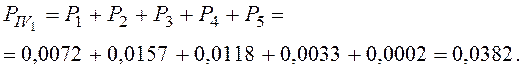
Это и есть вероятность  варианта оптимального плана формирования поездов.

4).  и . При этом .По теореме о полной вероятности (сумма всех элементарных вероятностей событий, образующих полную группу равна единице), можно подсчитать вероятность  варианта оптимального плана, когда каждый из потоков в отдельности меньше своих критических значений, но их сумма .

На основании проведенного статистического анализа плана формирования поездов можно сделать следующие выводы:

Первый вариант плана формирования поездов, рассчитанный по средним значениям вагонопотоков, будет оптимальным лишь 80 дней в году (). В остальные дни с вероятностью 0,1842 выгодно применение второго плана (67 дней в году), с вероятностью 0,3242 – применение третьего плана (118 дней в году), с вероятностью 0,0382 – применение плана  (14 дней в году) и с вероятностью 0,2393 – применение плана  ( 87 дней в году).

     Это означает, что для соблюдения оптимального режима работы по организации вагонопотоков на данном  полигоне целесообразно иметь двух-трехвариантных план формирования поездов (например, первый и третий варианты).