Составление планов формирования поездов на основе вероятностного анализа вагонопотоков

Теперь по теории полной вероятности (сумма всех вероятностей наступления событий равна единице) можно посчитать вероятность III варианта оптимального плана формирования поездов, когда каждый в отдельности из потоков меньше своих критических значений, но в сумме N1j + N4j > 260, т.е. больше критического значения для назначения поездов БГ.

Полученный результат свидетельствует о правильности выполненного вероятностного анализа плана формирования поездов в соответствии с заданием.

Вывод:

Первый вариант плана формирования поездов, рассчитанный по средним значениям вагонопотоков, будет оптимальным 148 дней в году (0,2937 • 365 = 108). В остальные дни с вероятностью 0,0064 выгодно применение третьего плана формирования (3 дня в году); с вероятностью 0,5645 – IV вариант (206 дней в году); с вероятностью 0,1354 – II вариант (49 дней в году). Это означает, что для соблюдения оптимального режима работы по организации вагонопотоков на полигоне АГ целесообразно иметь двухвариантный план формирования поездов (I вариант и IV вариант).

Зная критические значения вагонопотоков, необходимо организовать их суточный прогноз и в соответствии с ним строить работу по формированию поездов.

                                                          Задача № 2.

Тема: “Транспортная задача”.

Имеются три пункта отправления однородного груза, и пять пунктов его назначения. На пунктах отправления, груз находится в количестве , в пункты назначения требуется доставить соответственно  груза. Известна стоимость перевозки единицы груза из каждого пункта отправления в каждый пункт назначения (матрица D). Составить такой план перевозки, при котором необходимо вывезти все запасы груза, полностью удовлетворить все потребности и обеспечить при этом минимум затрат на перевозку.

Исходные данные.

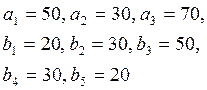
Решение.

Планом перевозок называется совокупность значений переменных удовлетворяющая системе линейных уравнений.

Теорема 1. Ранг r матрицы перевозок на единицу меньше числа уравнений в системе. Теорема является основополагающей для решения транспортной задачи.

Транспортная задача, как любая задача линейного программирования, может быть решена симплексным методом. Однако в силу простоты математической модели  специально для транспортной задачи разработаны более простые методы. Мы используем метод потенциалов. Применение метода потенциалов основано на понятиях опорного плана, цикла в матрице перевозок, потенциалов пунктов отправления и назначения, косвенных и истинных тарифов, критерия оптимальности плана перевозок.

Матрица перевозок.

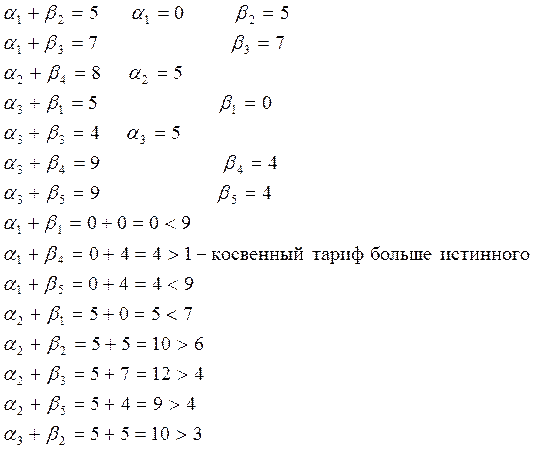
Определим общую стоимость перевозки грузов:

Цикл 1.

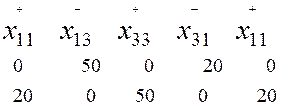
Определим стоимость перевозки грузов:

Поскольку С1 = 950> С = 810, то пересчет опорного плана по циклу 1 не привел к улучшению плана перевозок.

Цикл 2.

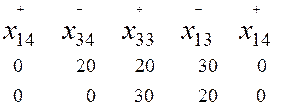
Определим общую стоимость перевозки грузов:

Поскольку С2 = 930> С = 810, то пересчет опорного плана по циклу 2 не привел к улучшению плана перевозок.

Цикл 3.

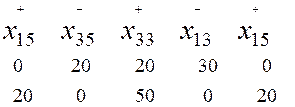
Определим общую стоимость перевозки грузов:

Поскольку С3 =870> С = 810, то пересчет опорного плана по циклу