Физика \ Физика

Законы постоянного тока. Правила Кирхгофа: Учебно-методическое обеспечение практического занятия

Страницы работы

14 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

интегральной форме следует обратить внимание на принципиальное различие между разностью потенциалов, электродвижущей силой и напряжением. Каждая из этих величин определяется как работа электрического поля по переносу единичного положительного заряда. Но разность потенциалов эта работа кулоновского потенциального поля, не зависящая от пути интегрирования. Электродвижущая сила – работа непотенциального стороннего поля, локализованного внутри источника, и поэтому зависит от пути интегрирования. Величина, численно равная работе, совершаемой электростатическими и сторонними силами над единичным положительным зарядом, называется падением напряжения или просто напряжением. На примере показать закон Ома для однородного и неоднородного участков цепи, зависимость омического сопротивления от геометрических размеров и свойств материала проводника, а также его изменение при последовательном и параллельном соединении проводников.

3.4.3. Рекомендуемая литература

[3] 4.1- 4.4.; [7] §2.

3.4.4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. По медному проводу сечением 1,00 мм² течет ток силой 10,0 мА. Найти среднюю скорость упорядоченного движения электронов вдоль проводника, если считать, что на каждый атом меди приходится один электрон проводимости.

Дано:

Решение

мм² м²;

мА А;

кг/моль;

кг/м³.

– ?

Средняя скорость упорядоченного движения электронов входит в формулу для плотности тока

, (1.1)

где – заряд электрона; – концентрация электронов.

Концентрация электронов

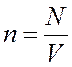. (1.2)

Число частиц в объеме

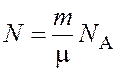, (1.3)

где – молярная масса; – число Авогадро.

Масса вещества в объеме

, (1.4)

где – плотность вещества.

Необходимые для расчетов данные о плотности меди и ее молярной массе находим в справочнике.

Подстановка выражений (1.3) и (1.4) в (1.2) дает

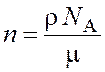. (1.5)

Плотность тока

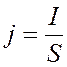. (1.6)

Подставим формулы (1.5) и (1.6) в уравнение (1.1):

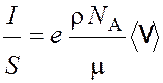откуда

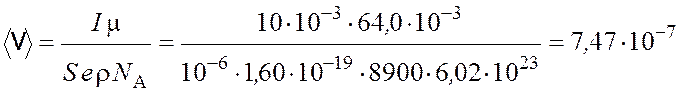м/с.

Ответ: м/с.

Пример 2. Внешняя цепь источника тока потребляет мощность Вт. Определить силу тока в цепи, если ЭДС источника тока В и внутреннее сопротивление Ом.

Дано:

Решение

Вт;

В;

Ом.

– ?

Мощность, потребляемая внешней цепью,

, (2.1)

где – падение напряжения во внешней цепи.

Закон Ома для замкнутой цепи позволяет найти это падение напряжения:

;

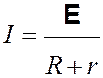. (2.2)

Объединяя формулы (17.1) и (17.2), имеем

откуда

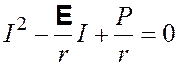Подставляем числовые значения, получаем следующее уравнение:

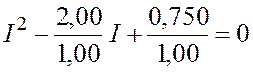Решение этого квадратного уравнения дает два корня:

А и А.

Оба корня имеют физический смысл, так как внешняя электрическая цепь может потреблять заданную мощность при двух различных значениях тока (при двух различных значениях сопротивления внешней цепи).

Ответ: А, А.

Пример 3. На сколько равных частей разрезали проводник сопротивлением 100 Ом, если после параллельного соединения отрезков их сопротивление стало равным 1,00 Ом?

Дано:

Решение

Ом;

Ом.

– ?

Сопротивление одного отрезка

, (3.1)

где – число частей, на которое разрезали проводник.

При параллельном соединении отрезков эквивалентное сопротивление рассчитывается по формуле

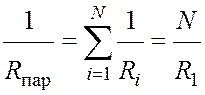. (3.2)

Подставив выражение (18.1) в уравнение (18.2), получим

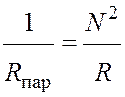или ,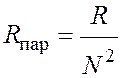

откуда

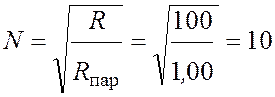Ответ: .

Пример 4. Прибор с ценой деления в 10,0 мкА имеет шкалу, содержащую 100 делений. Внутреннее сопротивление прибора 50,0 Ом. Как из этого прибора сделать вольтметр для измерения напряжения до 200 В или амперметр для измерения тока до 1,00 А?

Дано:

Решение

;

– ?

При отклонении стрелки прибора на всю шкалу (100 делений) через прибор протекает ток

Для измерения прибором напряжения его следует включить в схему так, как показано на рис. 19.1. Последовательно с прибором включают добавочное сопротивление .

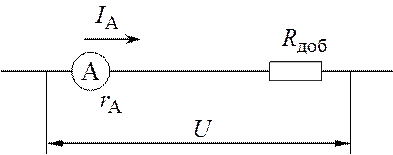
Рис. 4.1

Измеряемое напряжение частично падает на внутреннем сопротивлении прибора и частично – на добавочном сопротивлении . При этом через прибор может протекать ток не более , и стрелка прибора отклоняется на всю шкалу (100 делений):

откуда

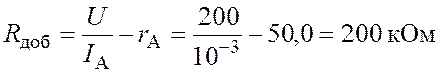При измерении прибором тока его следует включить в схему так, как показано на рис. 4.2.

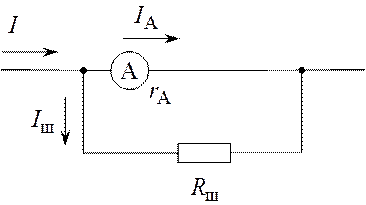Рис. 4.2

Параллельно прибору включают сопротивление шунта , по которому часть измеряемого тока идет в обход прибора. Через прибор может протекать ток не более , при котором стрелка отклоняется на всю шкалу:

. (4.1)

При таком включении падение напряжения на приборе и шунте будет одинаковым:

(4.2)

Из формул (4.1) и (4.2) получаем сопротивление шунта:

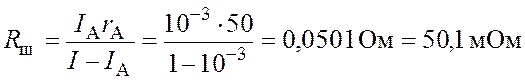Ответ: .

Пример 5. Определить ЭДС и внутреннее сопротивление аккумулятора, если при токе 15,0 А он отдает во внешнюю цепь мощность 135 Вт, а при токе 6,00 А – мощность 64,8 Вт.

Дано:

Решение

;

– ?

Внутренний участок цепи включает внутреннее сопротивление аккумулятора , внешнюю цепь составляет сопротивление нагрузки .

При изменении сопротивления изменяется ток в цепи и соответственно мощность, отдаваемая во внешнюю цепь (рис. 5.1).

Рис. 5.1

По закону Ома для замкнутой цепи имеем

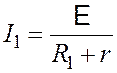; (5.1)

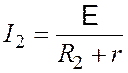, (5.2)

где и – сопротивления нагрузки для токов и .

Мощность, выделяемая на нагрузках:

; (5.3)

. (5.4)

Из формул (5.3) и (5.4) найдем числовые значения сопротивлений нагрузки:

;

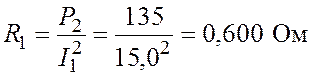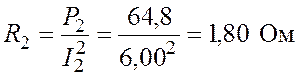Для определения внутреннего сопротивления аккумулятора r разделим уравнение (5.1) на уравнение (5.2), получим

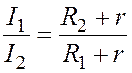откуда внутреннее сопротивление источника тока

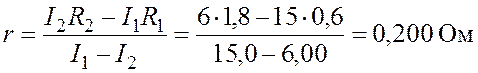Из уравнения (5.1) находим ЭДС источника тока:

Ответ: ; .

Пример 6. В схеме, изображенной на рис. 21.1: ЭДС источников равны и , сопротивления двух резисторов по , третьего – . Найти токи, текущие через сопротивления. Внутренним сопротивлением источников пренебречь.