Исследование процесса консервации биопрепаратов: Методические указания к лабораторной работе № 4 по курсу «Криогенные технологии в медицине и биологии», страница 3

где φ  – влагосодержание; r_в – теплота плавления воды; h₂₇₁ – энтальпия материала до начала дефростации.

Переход на использование в вычислениях энтальпий требует изменения методики расчетов. При замене производных разностными приближениями [2] уравнение энергии примет вид:

,     (6)

где h_i ,  h_i^¢ – соответственно текущее и последующее значение энтальпии в ί-точке; q_i+1 , q_i-1 – соответственно тепловой поток от предыдущей и последующей точек; q_v  –  тепловой поток от внутренних источников в объеме, отнесенном к ί-точке.

В рассматриваемой модели отсутствуют внутренние источники теплоты, т.е. не происходит химических превращений или физиологических процессов способных выделить теплоту, по этому:

                           ,                            (7)

После этого допущения можно разбить объект криогенного замораживания на систему из элементарных цилиндров и рассмотреть теплоту, поступающую к цилиндрам с центральной части к периферии объекта при помощи классических уравнений теплопроводности. Внешний подвод теплоты от точки расположенной за пределами рассматриваемого участка описывается выражением (8), а тепловой поток, подводимый из внутренней части к элементарному цилиндру описывается выражением (9).

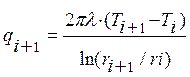               ,                   (8)

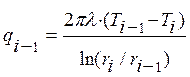               ,                   (9)

Решение дифференциального уравнения энергии  предполагает в себе определение величины тепловых потоков поступающих к рассматриваемому объекту с его границ т.к. объект замораживания представляет собой цилиндр то граница у этого цилиндра одна – эта граница объекта замораживания с ампулой контейнера, в котором он находится. Обмен между ампулой и объектом консервирования происходит в конвективном режиме [2]. Интенсивности конвективной передачи теплоты описывается  эффективным коэффициентом α*:

q_i+1 = a*×F×( T_к - T_i ),            (10)

Для центрального участка  выполняются все расчеты, с тем условием, что объект, от которого она могла получить теплоту, отсутствует:

q_i‑1 = 0,                       (11)

Решение дифференциального уравнения сводится к определению изменения энтальпий всех материальных точек для каждого последующего момента времени. Новое значение энтальпии обозначаем , и вычисляем его из материального баланса элементарной точки:

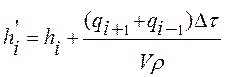                  .         (12)

После расчета новых значений энтальпий необходимо определить  соответствующие этим новым значениям значения температур T_i^' =f ( h_i^' ). Специфика решаемой задачи состоит в том, что объект криоконсервации может находиться в одном из трех энергетических состояний:

1.  Состояние первичного переохлаждения, когда температура объекта изменяется от температуры близкой к температуре окружающей среды до температуры начала кристаллизации. .

2.  Состояние кристаллизации или дефростации, когда при постоянной температуре происходит изменение энтальпии за счет отвода (подвода) теплоты кристаллизации. .

3.  Если объект подвергается переохлаждению от температуры дефростации до температуры прекращения замораживания..

Для материла в замороженном состоянии при h_i^'< h₂₇₁  температура определяется из выражения:

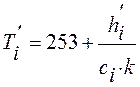                           ,                   (13)

где Т=253К – точка начала отсчета энтальпий.

Коэффициент к=0,5 учитывает, что в замороженном состоянии теплоемкость воды снижается в два раза.

На участке дефростации (14) температура постоянна T_i = const  или T_i = 271 K.

                       h₂₇₁< h_i^'< h₂₇₁+ φ r_в ,            (14)

где h₂₇₁  - минимальная энтальпия вещества подвергаемого дефростации;

φ·r_в  - теплота фазового перехода.

Для незамороженного слоя материала, т. е. при условии, что:

                          h_i^' > h₂₇₁  + φ r_в,                 (15)

температура определится из выражения:

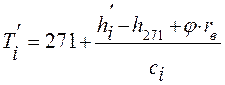                       ,         (16)

Моделируемая система, состоит из двух объектов охлаждения: препарата и контейнера. Для того чтобы математические вычисления не сопровождались ошибками, расчет тепловых полей в контейнере оформлен в виде самостоятельного модуля. При этом используется уравнение энергии (3), которое было применено при рассмотрении процессов протекающих в самом препарате.