Математическая модель исполнительного криотерапевтического комплекса, страница 2

Задачи, описывающие  перенос теплоты через многослойную структуру, обычно  решают с использованием дифференциального уравнения теплопроводности. Однако, учитывая, что уравнение теплопроводности получено путем преобразования уравнения энергии, а также наличие готовых программных продуктов, основанных на решении уравнения энергии, целесообразно и для изоляции воспользоваться этими решениями.

Вычисляется приращение теплосодержания в элементарных точках сетки разбиения. Значения температур получают по расчетным значениям энтальпий, поэтому исключаются нарушения элементарных тепловых балансов. 

При замене  производных разностными приближениями уравнение энергии примет вид:

,

где  h_i ,  h_i^¢ – соответственно текущее и последующее значение энтальпии в ί-точке;  q_i+1 , q_i-1 – соответственно тепловой поток от предыдущей и последующей точек; V  –  объем вещества, отнесенный  к       ί-точке.

Энергия подводимая к элементарной  точке теплопроводностью определяется как : , ,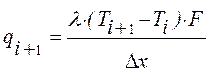

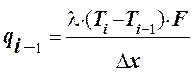где  Dx  – расстояние между точками (шаг разбиения); F – площадь, через которую переносится теплота (для одномерной модели                         F= DY×DZ=1×1=1).

К внутренней поверхности ограждения (i = 1)  теплота подводится  за счет конвективного теплообмена с теплоносителем:

q_i‑1 = a_вн× F×( T₁ - T_i ) ,

где  a_вн  – коэффициент теплоотдачи; T₁  – температура  теплоотводящей среды.

 К наружному слою (i = n_i)  теплота подводится атмосферным воздухом, температура воздуха =293 К:

q_i+1 = × F×( T_ос - T_i ) ,

Тепловые потоки к наружной и внутренней поверхности изоляции определяют граничные условия моделируемого процесса.

Начальные условия можно представить в виде:

при t = 0             T_3i  = T_ос.

       Вычисляя значения энтальпии на новом временном слое:

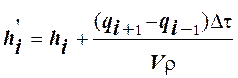
и по ним определяем  соответствующие значения температуры   T_i^' =f ( h_i^' ).

Алгоритм  вычислений реализован в виде подпрограммы WAND1.PAS. Подпрограмма содержит пусковой блок, который при первичном обращении  формирует массивы переменных, описывающих температуру и теплосодержание изоляции, а также передает в основную программу данные о физических свойствах.

 Для получения достоверных результатов перечисленные величины рассчитываются для каждой точки координатной сетки (x, t ).  

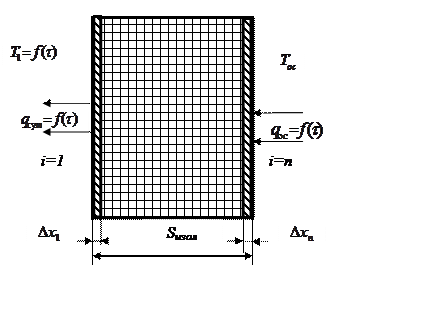Представленная на рис. 2.5.1 схема изоляции процедурной кабину не полно соответствует  конструкции теплового ограждения действующих криотерапевтических комплексов. В действительности конструкция  включает как минимум  еще два декоративных слоя, наружное и внутреннее покрытие (см. рис. 2.5.2).

Рис. 2.5.2 Схема теплового ограждения с наружным и внутренним декоративным покрытием.

Выбор материала для наружного покрытия не оказывает существенного влияния на эксплуатационные характеристики ограждения, внутренней покрытие попадает в зону колебания температуры изоляции, поэтому его физические свойства, теплоемкость, плотность и теплопроводность, имеют большое значение. Например, в групповых установках для внутреннего покрытия часто используют лиственные породы дерева []. Такой подход к исполнению декоративного покрытия является примером необоснованного распространения конструктивных решений используемых для обычных саун на криосауны. Сравнительно высокие значения теплопроводности, теплоемкости и плотности древесины, в сочетании  с толщиной доски, которая по конструктивным соображениям составляет не менее 15 мм, значительно увеличивают тепловую инерцию ограждения. Масса деревянного покрытия 25м² внутренней поверхности групповой кабины составляет около 250 кг. Дополнительные сложности создает проницаемость деревянного декоративного покрытия (см. рис. 2.5.3). Из-за неплотного сочленения досок криогенный теплоноситель омывает их со всех сторон и контактирует с теплоизоляционным материалом  стен.

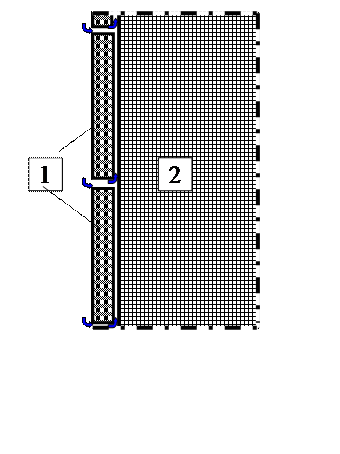Рис. 2.5.3 Схема внутренней отделки процедурной кабины деревянной доской. (1- доска, 2- теплоизолятор).