ІІ семестр
Індивідуальне завдання № 4
Тема: «Механічні і електромагнітні коливання. Змінний струм»
1. Період коливань крутильного маятника, який складається із кільця, з’єднаного спіральною пружиною з віссю обертання, дорівнює Т = 4 с. Визначити момент інерції цього маятника , якщо коефіцієнт жорсткості пружини К = 10-2 H/м. Тертям знехтувати.
![]()
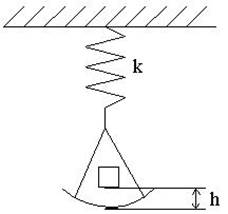 2. На шальку терезів, підвішену
на пружині, падає з висоти h тягар масою m і залишається на
шальці, не підскакуючи відносно неї. Шалька починає коливатися. Коефіцієнт
жорсткості пружини К. Визначити
2. На шальку терезів, підвішену
на пружині, падає з висоти h тягар масою m і залишається на
шальці, не підскакуючи відносно неї. Шалька починає коливатися. Коефіцієнт
жорсткості пружини К. Визначити
амплітуду А коливань (масою шальки і пружини порівняно з масою тягаря знехтувати).
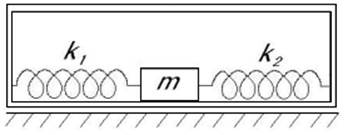 3.Тіло масою m
коливається без тертя всередені коробки масою M, яка лежить на
горизонтальній поверхні стола. До тіла прикріплені пружини з коефіцієнтами
жорсткості k1 і k2, кінці яких закріплені
на бокових стінках коробки. Визначити, при якій амплітуді коливань коробка
почне рухатися по поверхні стола, якщо коефіцієнт тертя між коробкою і столом
дорівнює m.
3.Тіло масою m
коливається без тертя всередені коробки масою M, яка лежить на
горизонтальній поверхні стола. До тіла прикріплені пружини з коефіцієнтами
жорсткості k1 і k2, кінці яких закріплені
на бокових стінках коробки. Визначити, при якій амплітуді коливань коробка
почне рухатися по поверхні стола, якщо коефіцієнт тертя між коробкою і столом
дорівнює m.
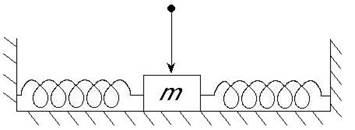 4. Брусок масою M лежить
на ідеально гладенькому столі і з’єднаний двома пружинами різної жорсткості з
опорами. Брусок коливається біля свого положення рівноваги.
4. Брусок масою M лежить
на ідеально гладенькому столі і з’єднаний двома пружинами різної жорсткості з
опорами. Брусок коливається біля свого положення рівноваги.
В момент, коли брусок проходить положення рівноваги, на нього зверху падає кусок пластиліну масою m і прилипає. Обчислити, у скільки разів зміниться період і амплітуда коливань.
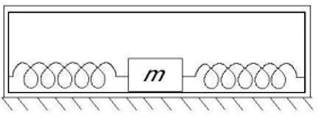 5. Тіло масою m
коливається без тертя всередині коробки масою M, яка лежить на
гладенькому столі. До тіла прикріпляються пружини однакової жорсткості, кінці
яких закріплені на бокових стінках коробки. Спочатку коробка закріплена, а
потім її відпустили і вона може вільно рухатися по столу. Визначити відношення частот
коливань в цих випадках.
5. Тіло масою m
коливається без тертя всередині коробки масою M, яка лежить на
гладенькому столі. До тіла прикріпляються пружини однакової жорсткості, кінці
яких закріплені на бокових стінках коробки. Спочатку коробка закріплена, а
потім її відпустили і вона може вільно рухатися по столу. Визначити відношення частот
коливань в цих випадках.
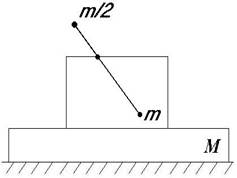 6. Маятник складається із двох
невеликих куль, з’єднаних стержнем довжиною l. Маси куль дорівнюють m
і m/2, вісь розташована на відстані l/3 від легкої кулі. Маятник
закріплений на платформі масою M = 3m, яка може ковзати без
тертя по горизонтальній поверхні. Визначити період малих коливань маятника.
6. Маятник складається із двох
невеликих куль, з’єднаних стержнем довжиною l. Маси куль дорівнюють m
і m/2, вісь розташована на відстані l/3 від легкої кулі. Маятник
закріплений на платформі масою M = 3m, яка може ковзати без
тертя по горизонтальній поверхні. Визначити період малих коливань маятника.
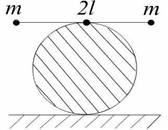 7.
На шорсткому нерухомому циліндрі радіусом R лежить (перпендикулярно його
твірній) невагома спиця довжиною 2l з двома кульками маси m на
кінцях. Знайти період малих коливань спиці.
7.
На шорсткому нерухомому циліндрі радіусом R лежить (перпендикулярно його
твірній) невагома спиця довжиною 2l з двома кульками маси m на
кінцях. Знайти період малих коливань спиці.
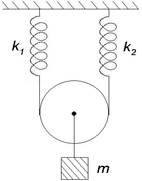
8. Знайти період коливань тягаря, підвішеного з допомо-гою невагомого блока і двох пружин з коефіцієнтами жорсткості k1 і k1. Знайти також максимальну амплітуду A коливань тягаря, при якій вони здійснюються ще по гармонічному закону.
9. Достатньо тонка пластинка із однорідного матеріалу має форму рівностороннього трикутника висотою h. Вона може обертатися навколо горизонтальної осі, яка співпадає з однією із сторін пластинки. Знайти період малих коливань T цього фізичного маятника.
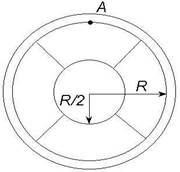 10. В центрі обруча масою m1
і радіусом R з допомогою легких спиць закріплено суцільну кулю радіусом R/2
і масою m2 = 2m1 . Обруч висить на гвіздку
A. Знайти період його малих коливань.
10. В центрі обруча масою m1
і радіусом R з допомогою легких спиць закріплено суцільну кулю радіусом R/2
і масою m2 = 2m1 . Обруч висить на гвіздку
A. Знайти період його малих коливань.
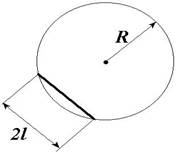 11. Однорідний стержень довжиною 2l
ковзає по гладенькому вертикальному колу радіусом R. Знайти період
малих коливань стержня.
11. Однорідний стержень довжиною 2l
ковзає по гладенькому вертикальному колу радіусом R. Знайти період
малих коливань стержня.
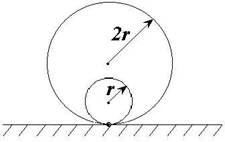 12. Обруч радіусом r
приварений до другого обруча такої ж маси та радіуса 2r. Система стоїть
на горизонтальному столі. Визначити період її малих коливань.
12. Обруч радіусом r
приварений до другого обруча такої ж маси та радіуса 2r. Система стоїть
на горизонтальному столі. Визначити період її малих коливань.
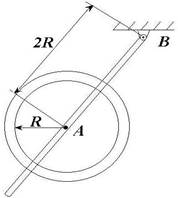 13. Маятник має вигляд обруча,
який висить на легенькій планці. Знайти період малих коливань маятника. Радіус
обруча дорівнює R. Відстань AB від центра обруча до точки підвісу
маятника дорівнює 2R.
13. Маятник має вигляд обруча,
який висить на легенькій планці. Знайти період малих коливань маятника. Радіус
обруча дорівнює R. Відстань AB від центра обруча до точки підвісу
маятника дорівнює 2R.
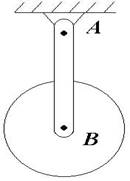 14. На кінці стержня довжиною l
і масою m прикріплений суцільний диск радіусом R і масою M.
Визначити період малих коливань стержня з диском навколо осі A, якщо
диск може вільно обертатися навколо осі B, що проходить через центр
диска.
14. На кінці стержня довжиною l
і масою m прикріплений суцільний диск радіусом R і масою M.
Визначити період малих коливань стержня з диском навколо осі A, якщо
диск може вільно обертатися навколо осі B, що проходить через центр
диска.
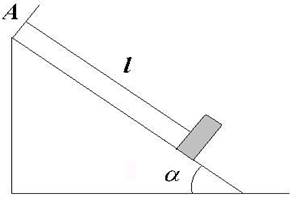 15. Тонкий диск, що котиться по
похилій площині, прикріплено до нерухомої точки A тонкою нерозтяжною
ниткою. Кут нахилу площини a
15. Тонкий диск, що котиться по
похилій площині, прикріплено до нерухомої точки A тонкою нерозтяжною
ниткою. Кут нахилу площини a![]() , довжина нитки l.
Диск котиться по площині без ковзання. Визначити період малих коливань диска.
Тертям кочення, товщиною диска та модулем кручення нитки знехтувати.
, довжина нитки l.
Диск котиться по площині без ковзання. Визначити період малих коливань диска.
Тертям кочення, товщиною диска та модулем кручення нитки знехтувати.
16. Знайти відношення періодів малих коливань T1/T2 однорідного кругового конуса, у якого радіус основи дорівнює висоті. В першому випадку конус шарнірно закріпили за вершину, у другому – за центр основи. В обох випадках вісь обертання горизонтальна.
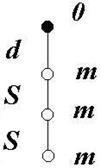
17. Легкий стержень може вільно обертатися навколо горизонтальної осі. На відстані d = 2см від осі на ньому закріплено невелику кульку і потім на відстані S = 3см одна від одної – ще дві такі самі кульки. Визначити період коливань цієї системи.
18. Кулю радіусом r = 7см підвішено на нитці довжиною l = 13см. Яку помилку ми робимо, вважаючи її за математичний маятник довжиною l1 = l + r?
19. Відомо, що енергія коливань камертона протягом часу t’ = 18c зменшилось у n = 105 раз. Знайти логарифмічний декремент затухання l. Частота коливань камертона n0 = 500Гц.
20. Стрілка чутливого приладу коливається біля положення рівноваги. Її послідовні крайні положення такі: n1 = 26,4; n2 = 10,7; n3 = 20,5. Знайти поділку, яка відповідає рівноважному положенню стрілки, якщо її декремент затухання є сталим у часі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.