Основи захисту відеоінформації: Методичні вказівки до лабораторних робіт, страница 2

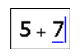
Для розширення охопленої куточком області можна користуватися клавішею "Пробіл":

Наступний уведений символ застосовується до всієї охопленої курсоромом області, так, наприклад, якщо виділено суму чисел і потім уводиться символ ділення "/", то в чисельнику виявляються обоє числа

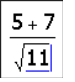
Для обчислення будь-якого вираження досить установити після нього оператор виводу (знак рівності =).

 

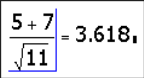
1.3. Змінні

Призначення змінних в MathCAD відповідає призначенню змінних у математиці. Змінні мають імена (ідентифікатори). Завдання змінним значень називається присвоюванням. Воно виконується оператором присвоювання :=, наприклад [3]:

A := 14.

Якщо змінній присвоюється значення оператором :=, то таке присвоювання є локальним. Однак за допомогою знака º визначається глобальне присвоювання. У цьому випадку змінна одержує задане значення незалежно від того, у якому місці документа стоїть оператор глобального присвоювання.

1.4. Ранжировані змінні

Часто виникає необхідність у завданні деякого впорядкованого ряду значень, для цього використовуються ранжировані змінні. Такі змінні мають множинні значення. Якщо потрібно задати ряд чисел із кроком d, то ранжирована змінна записується в такий спосіб [1]:

X := Xstart, Xstart + d .. Xend.

Тут Xstart – початкове значення змінної, Xend – кінцеве значення змінної.

1.5. Робота з масивами даних

Ранжирована змінна відрізняється від вектора тим, що неможливо використання її окремих значень – вона існує "вся відразу", до окремих її значень доступу немає. Для того щоб мати можливість доступу до кожного значення змінної з декількома компонентами, вона повинна бути задана у вигляді масиву – одномірного (вектора) або двомірного (матриці). У цьому випадку кожним елементом масиву можна оперувати як змінною.

Масив, як і будь-яка інша змінна, задається ім’ям. Місце розташування елемента визначається одним індексом для вектора або двома індексами для матриці. Для уведення індексу використовується знак "[" – пряма відкриваюча дужка. У відношенні індексованих змінних діють такі ж правила присвоювання і виводу, як і для звичайних змінних, наприклад:

, .

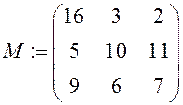1.6. Вбудовані функції

MathCad має безліч убудованих елементарних, спеціальних і статистичних функцій. Для полегшення уведення функцій на стандартній панелі інструментів є кнопка f(x), що виводить вікно з повним переліком функцій, розбитим на тематичні розділи. Нижче наведено короткий опис функцій, які використаються при виконанні лабораторних занять.

1.7. Тригонометричні і зворотні тригонометричні функції

sin(z), cos(z), tan(z) – синус, косинус і тангенс скалярного числа z, вимірюваного в радіанах.

asin(z), acos(z), atan(z) – арксинус, арккосинус і арктангенс скалярного числа z. Число, що повертає, виміряється в радіанах.

1.8. Функції комплексного аргументу

Re(z), Im(z) – виділення реальної і мнимої частин комплексного числа z;

arg(z) – обчислення аргументу комплексного числа z;

|z| – повернення модуля комплексного числа z.

1.9. Перетворення Фур'є

fft(v) – виконує БПФ для даних, представлених дійсними числами – значеннями вихідного вектора v, що має 2^m складових, де m – ціле число. У противному випадку виводиться повідомлення про помилку – невірному розмірі вектора. Повертає вектор, що складається з 1+2^m-1 елементів.

ifft(v) – реалізує зворотне БПФ для вектора v. Вектор повинен складатися з 1+2^m-1 елементів, де m – ціле число. Повертає вектор, що складається з 2^m елементів.

cfft(A) – виконує пряме перетворення Фур'є для вектора A з комплекс­ними елементами. Якщо A – матриця, реалізується двомірне перетворення.

icfft(B) – виконує зворотне перетворення Фур'є, при якому B є вектором або матрицею з комплексними елементами.

1.10. Функція умовних виразів

Синтаксис запису умовної функції виглядає в такий спосіб:

if (умова, вираз_1, вираз_2)

якщо в цій функції умова виконується, тоді буде обчислюватися і повертатися вираз_1, у противному випадку – вираз_2.

Приклад застосування функції if:

.

1.11. Векторні і матричні функції

length(V) – повертає кількість елементів вектора;