Основи захисту відеоінформації: Методичні вказівки до лабораторних робіт, страница 15

ЛАБОРАТОРНА РОБОТА № 16.
Стиск зображень на основі прогнозування

Мета роботи – вивчення алгоритмів стиску зображень на основі пророкування.

Завдання

Відновити зображення при різному числі рівнів квантування помилки пророкування.

Порядок виконання роботи

  1.  Відкрийте файл "len.bmp". Визначте кількість рядків, кількість стовпців зображення, виведіть зображення на екран.

  2.  Знайдіть нормовану кореляційну функцію R-зображення. Визначити по ній коефіцієнти однокрокової кореляції ,  і .

  3.  Напишіть функцію обчислення помилки пророкування [6]

,

використовуючи знайдені значення коефіцієнтів однокрокової кореляції:

-  вхідні дані: коефіцієнти однокрокової кореляції, вихідне зображення;

-  вихідні дані: масив помилки пророкування.

Зауваження: щоб спростити функцію, помилка не обчислюється для нульового рядка і нульового стовпця зображення.

  4.  Використовуючи функцію квантування зображення (заняття № 5), проквантуйте помилку пророкування на 2, 4 і 8 рівнів.

  5.  Напишіть функцію відновлення зображення [6]

-  вхідні дані: коефіцієнти однокрокової кореляції, проквантований масив помилок пророкування, нульовий рядок і нульовий стовпець вихідного зображення;

-  вихідні дані: відновлене зображення.

  6.  Відновіть зображення при різному числі рівнів квантування помилки пророкування, візуально оцінюючи якість відновлення.

Контрольні питання

  1.  Як визначити нормовану кореляційну функцію зображення?

  2.  Як визначити помилку прогнозуання?

  3.  Обгрунтуйте необхідність квантування помилки прогнозування.

  4.  Як створити функцію відновлення зображення?

  5.  Чим визначається якість відтвореного зображення при стискуванні методом прогноування?

Додаток 1. Завдання для залікового заняття

ВАРІАНТ № 1

Спотворіть зображення адитивним гаусовським шумом (). Напишіть процедуру лінійної фільтрації, що згладжує, зображення в просторовій області з використанням вікна: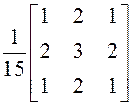. Обробіть перекручене зображнння.

ВАРІАНТ № 2

Спотворте зображення імпульсною перешкодою (інтенсивність перешкоди дорівнює 0.2). Напишіть процедуру медіанної фільтрації зображення, використовуючи всі 9 елементів вікна розміром  ел. Обробіть перекручене зображення.

ВАРІАНТ № 3

Спотворте зображення адитивним гаусовським шумом (). Напишіть процедуру лінійної фільтрації, що згладжує, зображення в частотній області з імпульсною характеристикою: 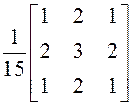 фільтра. Обробіть спотворене зображення.

ВАРІАНТ № 4

Напишіть процедури лінійної високочастотної фільтрації зображення (у вигляді окремих функцій) з використанням вікон: 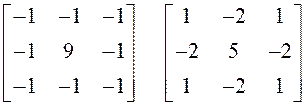. Обробіть вихідне зображення.

ВАРІАНТ № 5

Напишіть процедуру моделювання перекручування типу «змаз» у частотній області. Імпульсна характеристика фільтра, що спотворює

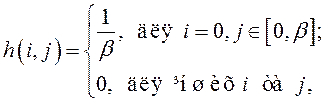
де  – величина змазу. Спотворте вихідне зображення.

ВАРІАНТ № 6

Напишіть процедуру моделювання перекручування типу "змаз" у просторовій області. Імпульсна характеристика спотворюючого фільтра

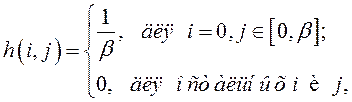
де  – величина змазу. Спотворте вихідне зображення.

ВАРІАНТ № 7

Напишіть процедуру розпізнавання зображень по критерію мінімуму середньоквадратичної помилки

,

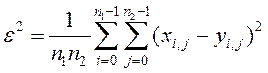де  – тестуєме зображення,  – еталонне зображення. Спотворте тестуєме зображення адитивним гаусовським шумом (). Виконайте процедуру розпізнавання зображення серед чотирьох еталонних зображень.

ВАРІАНТ № 8

Напишіть процедуру повороту зображення навколо довільної точки. Розміри перетвореного зображення повинні бути обрані таким чином, щоб повернене зображення не виходило за його краї. Поверніть зображення на 20⁰ навколо точки з координатами (40, 60).

ВАРІАНТ № 9

Напишіть процедуру перетворення гістограми зображення до експонентного виду. Характеристика передачі рівнів має вигляд:

,

де  – емпірична функція розподілу. Перетворіть зображення.

ВАРІАНТ № 10

Напишіть процедуру перетворення гістограми зображення до гіперболічного виду. Характеристика передачі рівнів

,

де  – емпірична функція розподілу. Перетворіть зображення.

ВАРІАНТ № 11