Основи захисту відеоінформації: Методичні вказівки до лабораторних робіт, страница 13

Мета роботи – вивчення методів виділення контурів за допомогою градієнтного методу і оператора Лапласа.

Завдання

Обчислити емпіричні функції розподілу для кожного із зображень із підкресленими контурами і перетворити їх в бінарні.

Порядок виконання роботи

  1.  Зчитайте файл "len.bmp". Визначить кількість рядків, кількість стовпців зображення, виведіть зображення на екран.

  2.  Напишіть функції для рішення завдання підкреслення контурів на зображеннях методом апроксимації градієнта [6]:

-  вхідні дані: вихідне зображення;

-  вихідні дані: зображення з підкресленими контурами.

  3.  Виконайте операцію підкреслення контурів за допомогою градієнтного методу і методу оператора Лапласа (лінійна маска ).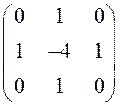

  4.  Обчислите емпіричні функції розподілу для кожного із зображень із підкресленими контурами і проведіть по них вибір порогів бінарізації.

  5.  Перетворіть зображення з підкресленими контурами в бінарні, використовуючи обрані пороги.

Контрольні питання

  1.  Які є методи завдання контурів зображення?

  2.  В чому полягає головна ідея методу апроксимації градієнта?

  3.  Як застосовується маска при операції підкреслення контурів?

  4.  Як обрати пороги бінарізації за емпіричними функціями розподілу?

  5.  Як використовуються пороги бінарізації?

ЛАБОРАТОРНА РОБОТА № 12.
Геометричні перетворення зображень

Мета роботи – вивчення методу геометричного перетворення зображень.

Вид перетворення [5]:

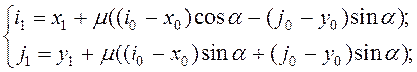
де  і  – просторові координати відрахунків вихідного і перетвореного зображень, ,,  і – параметри зрушень, масштабу і повороту.

Завдання

Перетворити зображення відповідно до заданих параметрів.

Порядок виконання роботи

  1.  Ознайомтеся з описом стандартних функцій: cos( ) і sin( ).

  2.  Зчитайте файл "face.bmp". Визначить кількість рядків, кількість стовпців зображення, виведіть зображення на екран.

  3.  Напишіть функцію геометричного перетворення зображень:

-  вхідні дані: вихідне зображення, параметри перетворення;

-  вихідні дані: перетворене зображення.

Зауваження: при перетворенні зображення необхідно контролювати вихід за межі зображення і округляти до цілого обчислені координати.

  4.  Задайте параметри перетворення: зрушення, масштаб, поворот.

  5.  Перетворіть зображення відповідно до заданих параметрів.

Контрольні питання

  1.  Які види систем координат існують?

  2.  В чому полягає і як застосовується геометричне перетворення зображень?

  3.  Які змінити масштаб зображення?

  4.  Як виконати поворот зображення?

  5.  Як виконати зсув зображення?

ЛАБОРАТОРНА РОБОТА № 13.
Розпізнавання зображень із використанням еталонів

Мета роботи – знайомство із задачею розпізнавання зображень на прикладі кореляційно-екстремального методу.

Завдання

Серед еталонів, представлених у вигляді бібліотеки, знайти зображення, найбільш схоже на тестуєме (вхідне), міра подібності – коефіцієнт взаємної кореляції.

Порядок виконання роботи

  1.  Відкрийте будь-які 4 з 9 файлів "1.bmp"…"9.bmp". Визначить кількість рядків, кількість стовпців для еталонних зображень. Виведіть еталонні зображення на екран. У якості тестуємого зображення використайте одне із зображень, не викреслюючи його із числа еталонів.

  2.  Напишіть функцію перекручування зображення адитивним гаусовським шумом з нульовим математичним очікуванням:

-  вхідні дані: вихідне зображення, відношення сигнал/шум 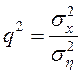, де  й  – дисперсії зображення і шуму відповідно [1];

-  вихідні дані: зображення, перекручене адитивним шумом.

  3.  Отримайте набір тестуємих зображень, спотворивши вихідне тестуєме зображення адитивним гаусовським шумом при , , , . Одне з тестуємих зображень перетворіть у негатив. Виведіть отримані зображення на екран.

  4.  Обчислить коефіцієнти взаємної кореляції між вихідним тестуємим зображенням і зображеннями, перекрученими шумом. Спостерігайте зменшення абсолютного значення коефіцієнта кореляції.