




Министерство образования и науки Украины
Национальный аэрокосмический университет им. Н.Е. Жуковского «Харьковский авиационный институт»
Кафедра 304
Лабораторная работа №3
По курсу «Численные методы»
По теме: «Приближенное вычисление определенных интегралов»
Выполнил:
студент 325 группы
Меняйлов Евгений
Проверила:
Яровая О.В.
___________________
Харьков 2010
Теоретические сведения
Ручной счет
Лабораторная работа №3
«Приближенное вычисление определенных интегралов»
Цель
работы.Вычислить
заданный определённый интеграл 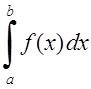 по формулам трапеций, Симпсона,
средних, правых, левых прямоугольников при
по формулам трапеций, Симпсона,
средних, правых, левых прямоугольников при ![]() .Оценить
погрешность полученных результатов.
.Оценить
погрешность полученных результатов.
Программная реализация в MathCad.
|
Исходные данные. |
|
|
|
|
|
|
|
|
|
2. Вычисление определенного интеграла с помощью стандартной функции. |
|
|
|
3. Программный блок, реализующий вычисление приближенного значения определенного интеграла. 1. Формула Симпсона. 2. Формула трапеций. 3. Формула средних прямоугольников. 4. Формула правых прямоугольников. 5. Формула левых прямоугольников. |
|
1. Табулирование функции на заданном промежутке [a,b]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Вычисление априорной погрешности вычислений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Вычисление апостериорной погрешности вычислений. |
|
|
|
|
|
|
Программная реализация в MatLab.
Вычисление определенного интеграла с помощью встроенной функции.
>> I = double(int((x^2+1.8)/(x^3+7.9),2,4.4))
I =
0.71276735214085
Программный блок, реализующий приближенное вычисление определенного интеграла.
function res = f(x);
res = (x^2+1.8)/(x^3+7.9);
end
----------------------
function res = Integral(str, a , b, n);
%str - methods name, a,b - distance, n - number of points
h = (b-a)/n;
Sum = 0;
switch (str)
case 'Simpson'
q1=0; q2=0;
for i = 1:n-1
if (mod(i,2)==1)
q1 = q1+f(a + i*h);
else q2 = q2+f(a + i*h);
end;
end;
Sum =(h/3)*( f(a) + 4*q1 + 2*q2 + f(b));
case 'Trapezium'
for i = 1:n-1
Sum = Sum + f(a + i*h);
end;
Sum = (h/2)*( f(a) + 2*Sum + f(b));
case 'LeftRectangles'
for i=1:n-1
Sum = Sum + h*f(a + i*h);
end;
Sum = h*f(a) + Sum;
case 'RightRectangles'
for i=1:n-1
Sum = Sum + h*f(a + i*h);
end;
Sum = h*f(b) + Sum;
case 'MediumRectangles'
for i=1:n
Sum = Sum + h*f(((a + (i-1)*h)+(a + i*h))/2);
end;
otherwise
error('This is impossible value')
end
res = Sum;
return
----------------------------------------------------------------------------------------
Результатывычислений.
>> format long
>> IS = Integral('Simpson',2,4.4,12)
IS =
0.71276572838571
>> IT = Integral('Trapezium',2,4.4,12)
IT =
0.71268919512492
>> IRR = Integral('RightRectangles',2,4.4,12)
IRR =
0.69894336360573
>> ILR = Integral('LeftRectangles',2,4.4,12)
ILR =
0.72643502664411
>> IMR = Integral('MediumRectangles',2,4.4,12)
IMR =
0.71280628137761
-------------------------------------------------
Программный блок, реализующий вычисления априорной погрешности.
function res = Priori_Error(str,a,b,n);
switch (str)
case 'Simpson'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n))/15;
case 'Trapezium'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n))/3;
case 'LeftRectangles'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n));
case 'RightRectangles'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n));
case 'MediumRectangles'
R = abs(Integral(str,a,b,n)-Integral(str,a,b,0.5*n))/3;
otherwise
error('This is impossible value')
end;
res = R;
return
-------------------------------------------------
Результатывычислений.
>> Priori_ErrorIS = Priori_Error('Simpson',2,4.4,12)
Priori_ErrorIS =
6.09223154409324e-004
>> Priori_ErrorIT = Priori_Error('Trapezium',2,4.4,12)
Priori_ErrorIT =
0.02974307927841
>> Priori_ErrorIRR = Priori_Error('RightRectangles',2,4.4,12)
Priori_ErrorIRR =
0.02984543130157
>> Priori_ErrorILR = Priori_Error('LeftRectangles',2,4.4,12)
Priori_ErrorILR =
0.08923623173681
>> Priori_ErrorIMR = Priori_Error('MediumRectangles',2,4.4,12)
Priori_ErrorIMR =
3.08922898968129
-------------------------------------------------
Программный блок, реализующий вычисления апостериорной погрешности.
function res = R(str,a,b,n);
M = zeros(n+1,1);
h = (b-a)/n;
ch = [0 1 0 1.8];
zn = [1 0 0 7.9];
switch (str)
case 'Simpson'
[q,d] = polyder(polyder(polyder(polyder(ch,zn))));
for i = 1:n+1
M(i,1) = polyval(q,a + (i-1)*h)/polyval(d,a + (i-1)*h);
end;
R = abs(((b-a)*max(abs(M))*(h^4))/180);
case 'Trapezium'
[q,d] = polyder(polyder(ch,zn));
for i = 1:n+1
M(i,1) = polyval(q,a + (i-1)*h)/polyval(d,a + (i-1)*h);
end;
R = abs(((b-a)*(h^2)*max(abs(M)))/12);
case 'LeftRectangles'
[q,d] = polyder(ch,zn);
for i = 1:n+1
M(i,1) = polyval(q,a + (i-1)*h)/polyval(d,a + (i-1)*h);
end;
R = abs((b-a)*h*max(abs(M)));
case 'RightRectangles'
[q,d] = polyder(ch,zn);
for i = 1:n+1
M(i,1) = polyval(q,a + (i-1)*h)/polyval(d,a + (i-1)*h);
end;
R = abs((b-a)*h*max(abs(M)));
case 'MediumRectangles'
[q,d] = polyder(polyder(ch,zn));
for i = 1:n+1
M(i,1) = polyval(q,a + (i-1)*h)/polyval(d,a + (i-1)*h);
end;
R = abs(((b-a)*(h^2)*max(abs(M)))/6);
otherwise
error('This is impossible value')
end;
res = R;
return
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.