Решение интегральных уравнений Фредгольма, Вольтера методом конечных сумм

function res  = Integral_equation(a,b,n,N,str);

h = (b-a)/(n-1); %шаг

lambda = 8; % параметр

%1. Табулирование значений

vx = zeros(n,1);

vy = zeros(n,1);

for i=1:n

    vx(i) = a + (i-1)*h;

    vy(i) = F(vx(i));

end;

%2. Формируем весовые коэффициенты для формулы N

A = zeros(n,1);%матрица весовых коэффициентов

switch (N)  %формула Симпсона

    case 1

        A(1) = h/3;

        A(n) = h/3;  

        for i = 2:n-1

            if (mod(i,2)==0)

                A(i) = 4*h/3;

            else  A(i)=2*h/3;

            end;

        end;

    case 2  %формула трапеций

        A(1) = h/2;

        A(n) = h/2;

        for i = 2:n-1

            A(i) = h;

        end;

    case {3, 4} %формулы правых и левых прямоугольников

        for i = 1:n

            A(i) = h;

        end

    otherwise error('This is impossible value')

end;

%3. Формирование матрицы коэффициентов

D = zeros(n,n);

switch (str)

    case 'Fredgolm'%   для уравнения Фредгольма

            for i=1:n

                for j=1:n

                    if (i == j) D(i,j) = 1-lambda*A(j)*k(vx(i),vx(j));

                    else D(i,j) = -lambda*A(j)*k(vx(i),vx(j));

                    end;

                end;

            end;

    case 'Volter'% Вольтера

            for i=1:n

                for j=1:n

                    if ((i==j) && (vx(j)<=vx(i))) D(i,j) = 1-lambda*A(j)*k(vx(i),vx(j));

                    end;

                    if ((i ~= j) && (vx(j)> vx(i))) D(i,j) = -lambda*A(j)*k(vx(i),vx(j));

                    end;

                end;

            end;

end;

% 4. Вычисление значений искомой функции в узловых точках

y = inv(D)*vy;

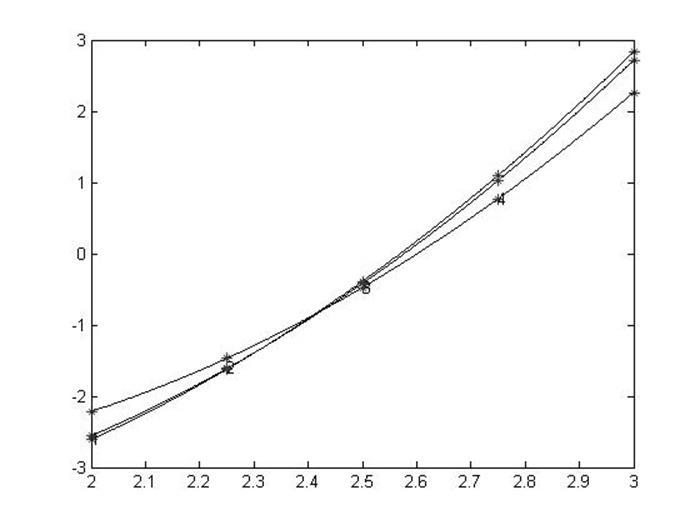
% 5. Построение графика искомой функции fi(х) на интервале [a,b];   

VR=zeros(1000,1);

X=linspace(a,b,1000);

for i=1:1000

    VR(i) = fi(X(i),lambda,y,vx,A);

end;

plot(X,VR,'-k'),hold on,plot(vx,y,'*r'),hold on;

text(vx(N),y(N),int2str(N),'FontSize',10);

% 6. Проверка вычислений. left side of equation

syms x t;

G = fi(x,lambda,y,vx,A) - lambda*int(k(x,t)*fi(t,lambda,y,vx,A),t,a,b)

res = VR;             

return

-------------------------------------------------------------------------------------

function res = F(x);

% источник интегрального уравнения

         res = 2*x^2-x+1;

return

function res = fi(x,lambda,y,vx,A);

Int=0;

for i=1:length(vx)

    Int = Int + A(i)*k(x,vx(i))*y(i);

end;

res = F(x)+ lambda*Int;

return

function res = k(x,t);

% ядро интегрального уравнения

         res = 2*x+3*t;

return

-------------------------------------------------------------------------------------

Результатывычислений.

>> fi1 = Integral_equation(2,3,5,1,'Fredgolm');

G =

 2*x^2-73746443898103597/73746443898191872*x+884957326782296239/884957326778302464

 >> fi2 = Integral_equation(2,3,5,2,'Fredgolm');

G =

 2*x^2-2/3*x+1927/540

>> fi3 = Integral_equation(2,3,5,3,'Fredgolm');

G =

2*x^2-383931868233635645/672162244385046528*x+9359605925581220903/896216325846728704

>> fi4 = Integral_equation(2,3,5,4,'Fredgolm');

G =

2*x^2-383931868233635645/672162244385046528*x+9359605925581220903/896216325846728704

>> fi1 = Integral_equation(2,3,5,1,'Volter');

G =

2*x^2-143411772403022304887/2168483220578893824*x-394725987733825442047741/1509264321522910101504

>> fi2 = Integral_equation(2,3,5,2,'Volter');

 G =

 2*x^2-55459020103150102008349/862151098265298272256*x-219553549192232887894979/862151098265298272256

>> fi3 = Integral_equation(2,3,5,3,'Volter');

G =

2*x^2-5213686458210793469705/83064391527221428224*x-27546909973828092116393/110752522036295237632

>> fi4 = Integral_equation(2,3,5,4,'Volter');

 G =

2*x^2-5213686458210793469705/83064391527221428224*x-27546909973828092116393/110752522036295237632