«ХАИ»
Решение алгебраических и трансцендентных уравнений комбинированным методом
Цель: вычислить
комбинированным методом с точностью до ![]() действительный
корень заданного уравнения.
действительный
корень заданного уравнения.
Вычислительная схема:
1. Графически найти интервал изоляции корня для заданного уравнения
2. Нахождение корня уравнения методом хорд:
![]()
![]() - интервал изоляции корня уравнения
- интервал изоляции корня уравнения
Неподвижной является точка, в которой знак функции и второй производной совпадает.
Расчётная формула:
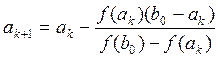
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
![]()
3. Нахождение корня уравнения методом Ньютона (метод касательных):
![]()
![]() - интервал изоляции корня уравнения
- интервал изоляции корня уравнения
Неподвижной является точка, в которой знак функции и второй производной совпадает.
Расчётная формула:
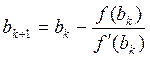
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
![]()
4. Нахождение корня уравнения модифицированным методом Ньютона:
![]()
![]() - интервал изоляции корня уравнения
- интервал изоляции корня уравнения
Неподвижной является точка, в которой знак функции и второй производной совпадает.
Расчётная формула:
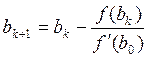
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
![]()
5. Нахождение корня уравнения методом секущих:
Если итерации ![]() и
и ![]() достаточно близки друг к другу то,
производная
достаточно близки друг к другу то,
производная ![]()
в алгоритме Ньютона можно заменить её приближённым значением в виде отношения:
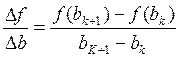
Для использования этого метода необходимо знать два
начальных приближения ![]() и
и ![]() .
.
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
![]()
6. Нахождение корня уравнения комбинированным методом:
![]()
![]() - интервал изоляции корня уравнения
- интервал изоляции корня уравнения
Расчётные формулы:
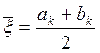
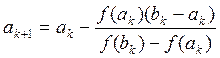
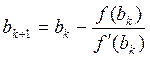
Вычисления до заданной точности проводятся, пока не выполнится неравенство:
![]()
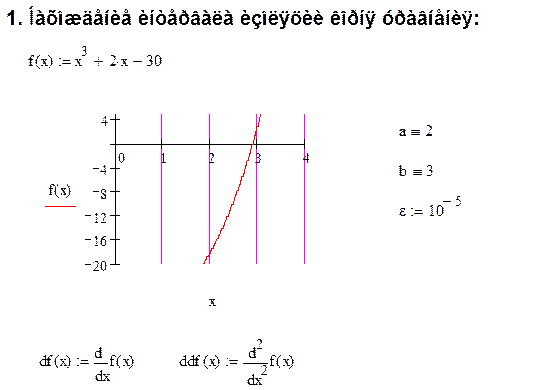
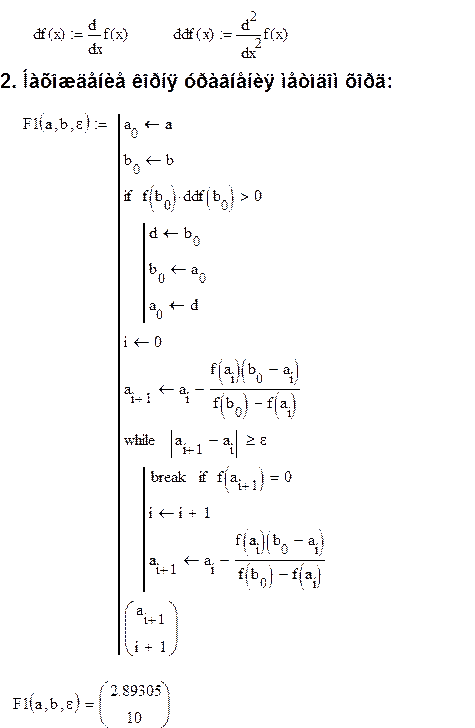
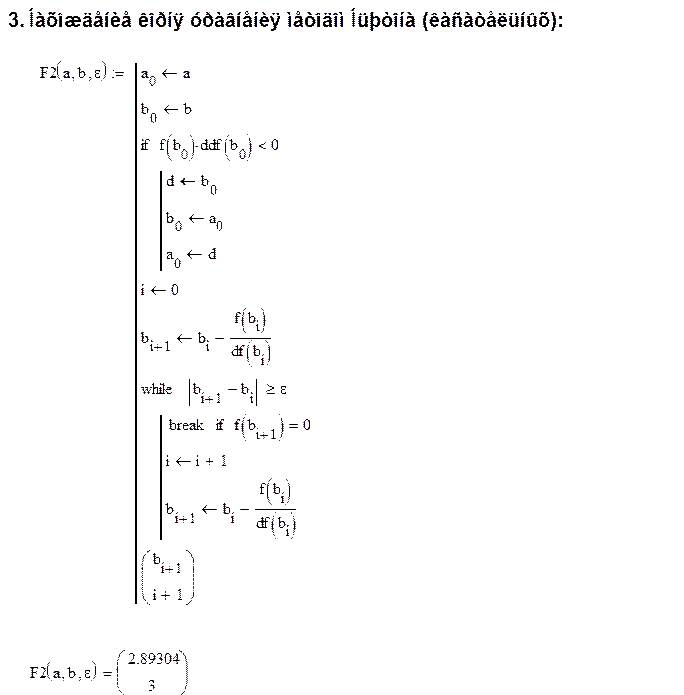
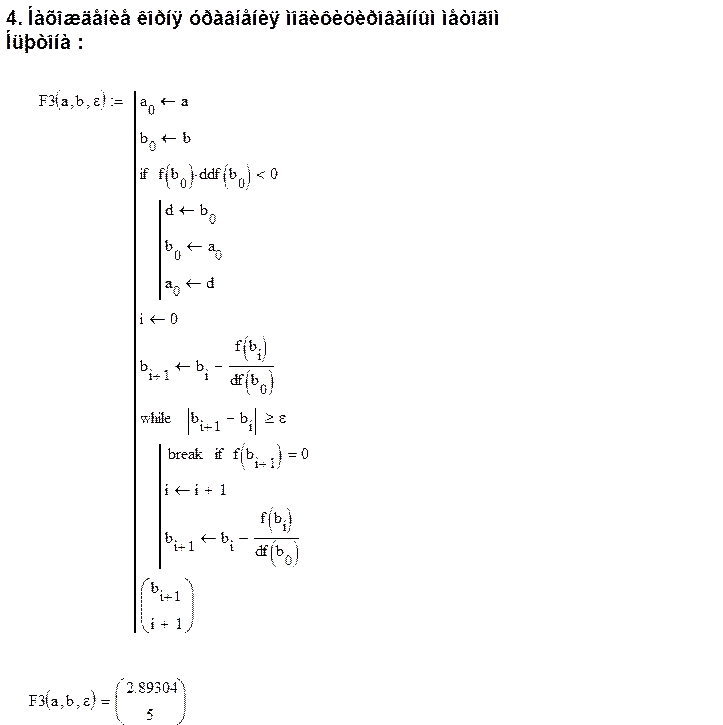
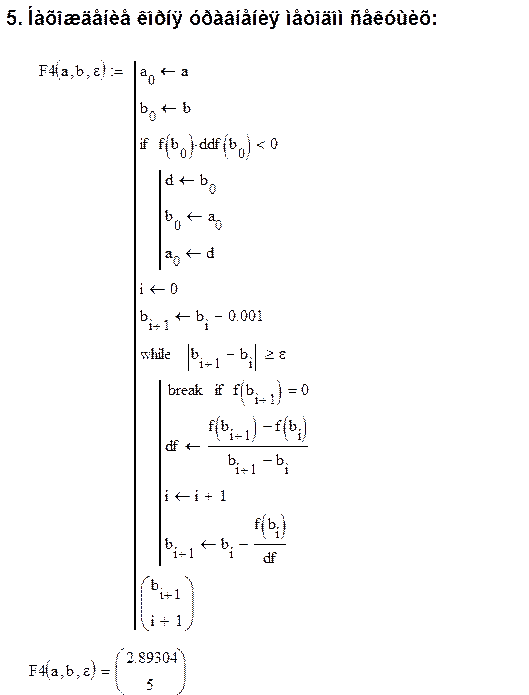
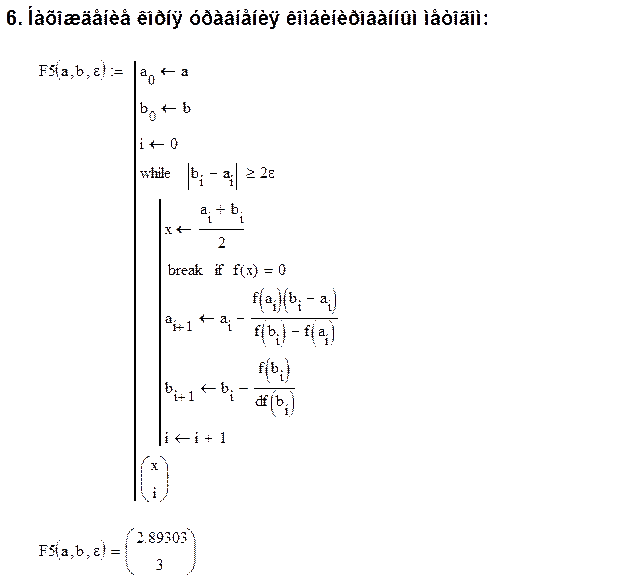
Результаты:
Метод |
Корень |
Кол-во итераций |
|
Метод хорд |
2.89305 |
10 |
|
Метод Ньютона |
2.89304 |
3 |
|
Модифицированный метод Ньютона |
2.89304 |
5 |
|
Метод секущих |
2.89304 |
5 |
|
Комбинированный метод |
2.89303 |
3 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.