Интерполирование для таблиц с постоянным шагом. Численное дифференцирование. Обратное интерполирование

Министерство образования и науки Украины

Национальный аэрокосмический  университет им. Н.Е. Жуковского

«Харьковский авиационный институт»

Кафедра 304

Лабораторная работа №5

По курсу «Численные методы»

По теме:  «Интерполирование для таблиц с постоянным шагом.

Численное дифференцирование. Обратное интерполирование.»

Выполнил:

студент 325 группы

Меняйлов Евгений

Проверила:

Яовая О.В.

___________________

Харьков 2009

Цель. Для табличной функции f(x), построить аналитическую функцию в виде интерполяционного многочлена Ньютона, Гаусса.  

Реализация в MathCad

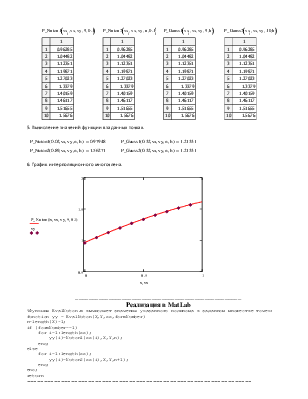
5. Вычисление значений функции в заданных точках.

6. График интерполяционного многочлена.

__________________________________________________

Реализация в MatLab

%Функция EvalNuton.m вычисляет значения указанного полинома в заданном множестве точек:

function yy = EvalNuton(X,Y,xx,formNumber)

n=length(X)-1;

if (formNumber==1)

    for i=1:length(xx);

        yy(i)=Nuton1(xx(i),X,Y,n);

    end;

else

    for i=1:length(xx);

        yy(i)=Nuton2(xx(i),X,Y,n+1);

    end;

end;

return

------------------------------------------------------------------

%X,Y – табличные значения; x – точка интерполяции; n – количество узловых точек.

function res = Nuton1(x,X,Y,n);

res=Y(1);

% определение шага таблицы

h=X(2)-X(1);

for i=1:n

    % построение матрицы конечных разностей

    konrazn=diff(Y,i);

    konrazn=konrazn(1);

    % вычисление факториала

    fact=prod(1:i);

    % вычисление (x-x0)(x-x1)...(x-xn-1)

    Mult=1;

    for j=1:i

        Mult=Mult*(x-X(j));

    end;

    res=res+(konrazn/(fact * h^i))*Mult;

end;

return

------------------------------------------------------------------

function res = Nuton2(x,X,Y,n);

res=Y(n);

% определение шага таблицы

h=X(2)-X(1);

%определение q

q=(x-X(n))/h;

for i=1:(n-1)

    % построение матрицы конечных разностей

    konrazn=diff(Y,i);

    konrazn=konrazn(n-i);

    % вычисление факториала

    fact=prod(1:i);

    % вычисление q (q-1)(q-2)...(q-(i-1))

    Mult=1;

    for j=0:(i-1)

        Mult=Mult*(q+j);

    end;

    res=res+(konrazn/fact)*Mult;

end;

return

-------------------------------------------------

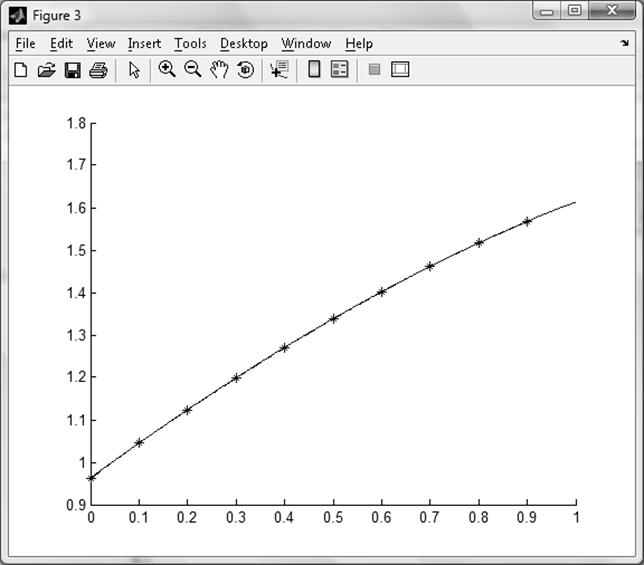
Построение графика интерполяционного многочлена.

xx=linspace(0,1,1000);

yy=EvalNuton(x,y,xx,1);

figure('Color','w');

hold on;

plot(xx,yy,'-b');

plot(x,y,'-.b*');

-------------------------------------------------------------------

Результаты.

>> x = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9];

>> y = [0.96285 1.04482 1.12351 1.19871 1.27023 1.33790 1.40159 1.46117 1.51655 1.5676];

>> EvalNuton(x,y,0.02,1)

ans =

    0.97948373715354

>> EvalNuton(x,y,0.89,2)

ans =

   1.56270742560460

function yy = EvalGauss(X,Y,xx,formNumber)

n=length(X)-1;

if (formNumber==1)

    for i=1:length(xx);

        yy(i)=Gauss1(xx(i),X,Y,n);

    end;

else

    for i=1:length(xx);

        yy(i)=Gauss2(xx(i),X,Y,n+1);

    end;

end;

return

---------------------------------------------------

function res = Gauss1(x, X, Y, n)

k = round(n/2);

res = Y(k);

% определение шага таблицы

h=X(2)-X(1);

for i=1:n

    % построение матрицы конечных разностей

    konrazn=diff(Y,i);

    konrazn=konrazn(k-floor(i/2));

    % вычисление факториала

    fact=prod(1:i);

    Mult=1;

    for j=1:i

        Mult=Mult*(x-X(k+(-1)^j*floor(j/2)));

    end;

    res=res+(konrazn/(fact * h^i))*Mult;

end;

return

---------------------------------------------------

function res = Gauss2(x, X, Y, n)

k = round(n/2);

res = Y(k);

% определение шага таблицы

h=X(2)-X(1);

for i=1:(n-1)

    % построение матрицы конечных разностей

    konrazn=diff(Y,i);

    konrazn=konrazn(k-floor(i/2));

    % вычисление факториала

    fact=prod(1:i);

    Mult=1;

    for j=0:(i-1)

        Mult=Mult*(x-X(k+(-1)^j*floor((i-j)/2)));

    end;

    res=res+(konrazn/(fact * h^i))*Mult;

end;

return

------------------------------------------------------------

       Результаты.

>> EvalGauss(x,y,0.32,1)

ans =

   1.21331463672730

>> EvalGauss(x,y,0.32,2)

ans =

   1.21331463672730

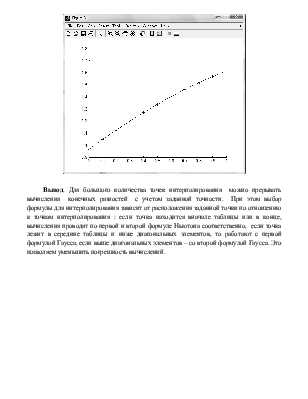
Вывод. Для большого количества точек интерполирования  можно прерывать  вычисления  конечных разностей  с учетом заданной точности.  При этом выбор формулы для интерполирования зависит от расположения заданной точки по отношению к точкам интерполирования : если точка находится вначале таблицы или в конце, вычисления проводят по первой и второй формуле Ньютона соответственно,  если точка лежит в середине таблицы и ниже диагональных элементов, то работают с первой  формулой Гаусса, если выше диагональных элементов – со второй формулой Гаусса. Это позволяем уменьшить погрешность вычислений.