Создание модели объекта управления (Лабораторная работа № 3)

Лабораторная работа №3

Создание модели объекта управления

Цель работы:

1.  Изучить принципы построения математических моделей технических объектов.

2. Выполнить построение математической модели объекта управления в среде Simulink пакета MatLab.

3. Экспериментально проверить работоспособность полученной модели.

Знания, полученные при выполнении лабораторной работы:

·  освоение математического аппарата и создания на его основе математической модели объекта управления;

·  моделирование работы объекта управления в среде Simulink пакета инженерного проектирования MatLab;

·  освоение принципов верификации математической модели объекта управления.

Ключевые слова:

линейные дифференциальные уравнения с постоянными коэффициентами, объект управления, объект регулирования, имитационное моделирование, ПИ-регулятор, запорно-регулирующая арматура,  интегрирующее звено, сумматор, функция Хэвиссайда, возмущающее воздействие, настройки регулятора.

Содержание лабораторной работы

1.  Общее описание

          Большинство объектов управления (регулирования) могут быть описаны линейными дифференциальными уравнениями с постоянными коэффициентами. Основываясь на описании объекта регулирования, заданного  дифференциальным уравнением второго порядка, рассмотрим этапы построения модели объекта регулирования. Модель процесса регулирования в лабораторной работе выполняется в виде ПИ-регулятора, который совместно с моделью запорно-регулирующей арматуры является замкнутой системой автоматического регулирования.

2. Методические указания

В лабораторной работе рассматривается объект, у которого входным воздействием является параметр  - u_n, а выходная величина x (рис.3.1).

Рис. 3.1 Описание объекта

Известно, что в результате экспериментов по исследованию динамики объекта получено следующее дифференциальное уравнение, описывающее изменение x(t) в зависимости от изменения возмущающей функции u_n(t):

                                     a_2*x”(t)+ a_1*x’(t) + a_0*x(t)= b_0*u(t),                            (3.1)

где

x(t) – выходной параметр объекта;

u (t) – входной параметр объекта;

a_2, a_1, a_0, b₀– коэффициенты дифференциального уравнения.

Возмущающая функция u_n(t) является известной функцией времени. Также заданы начальные условия, т.е. в начальный момент времени для объекта известны x|_t=0и  x’|_t=0.

В лабораторной работе необходимо решить дифференциальное уравнение – значит получить функцию x(t), меняющуюся во времени. Для составления структурной схемы решения применим метод понижения порядка производной, который сводится к следующим этапам.

Этап I.Разрешим дифференциальное уравнение относительно высшей производной

Этап II: Предположим (рис. 3.2), что в точке А значение x”(t) известно в любой момент времени, с помощью интегрирующего звена и с учетом начальных условий получим в точке В значение x’(t). Затем, с помощью еще одного интегратора , в точке С получим значение искомой функции x(t).

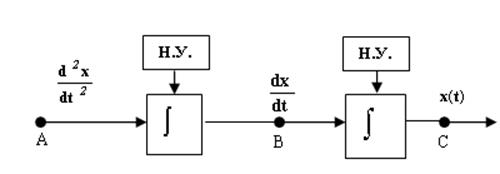
Рис. 3.2  Интегрирующие звенья

Этап III.Обратим теперь внимание на правую часть уравнения (3.2). Она представляет собой сумму трех функций времени u(t), x’(t) и x(t), взятых с постоянными коэффициентами. Функция u(t) - известная функция времени по условию лабораторной работы.

Допустим, рис. 3.3, что нам известны функции x(t) в точке С₁ и x’(t) в точке В₁. Теперь, просуммировав их с коэффициентами, соответствующими правой части, получим вторую производную x”(t). Таким образом, на выходе сумматора, в точке A₁, будет величина x”(t), известная в любой момент времени.

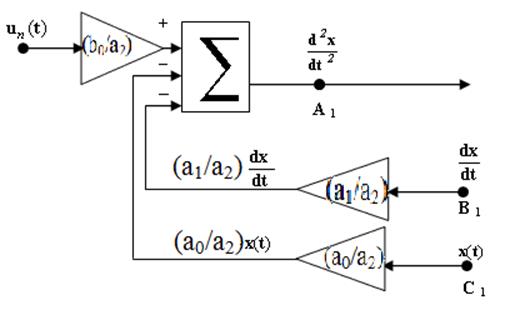
Рис. 3.3  Разомкнутая схема

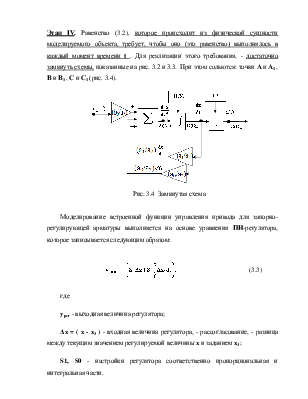
Этап IV. Равенство (3.2), которое происходит из физической сущности моделируемого объекта, требует, чтобы оно (это равенство) выполнялось в каждый момент времени t . Для реализации этого требования, - достаточно замкнуть схемы, показанные на рис. 3.2 и 3.3.  При этом сольются: точки А и А₁ , В и В₁ , С и С₁ (рис. 3.4).

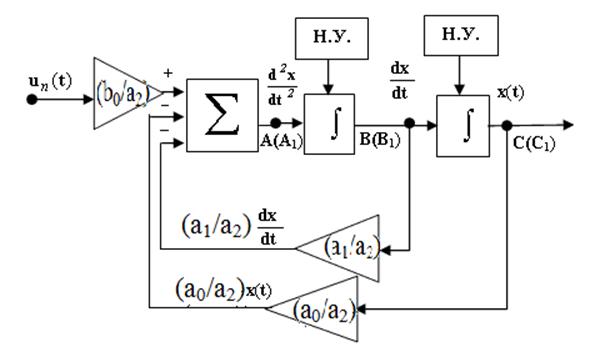
Рис. 3.4  Замкнутая схема

Моделирование встроенной функции управления привода для запорно-регулирующей арматуры выполняется на основе уравнения ПИ-регулятора, которое записывается следующим образом:

где

y_рег - выходная величина регулятора;

Δx = ( x - x₃ ) - входная величина регулятора, - рассогласование, - разница между текущим значением регулируемой величины x и заданием x₃;