Математика \ Математическая логика и теория алгоритмов

Математическая логика и теория алгоритмов: Учебное пособие

Страницы работы

67 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Пользуясь дедукцией (точнее, обратной теоремой дедукции), это правило можно записать в виде , либо в виде правила вывода метода резолюции:

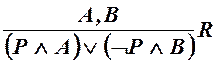Этим правилом вывода, доказанным вполне строго, можно пользоваться наряду с правилом МР.

Знаменатель правила имеет название «резольвента».

2.3. Исчисление предикатов

Пусть – произвольное множество. Предположим, что на нем задана тотальная функция (однозначное отображение) на этом множестве : (однозначное отображение), т.е. . Эта функция является -парной (или -местной).

Предположим, таких функций несколько: . Этот набор называется сигнатурой, что обозначается как . Пара (, ) называется алгеброй. Если функции сигнатуры являются произвольными отношениями, то пара (, ) называется моделью.

Примеры:

1. Пусть – множество целых чисел. Рассмотрим сигнатуру, состоящую из двух бинарных операций: « + », « * ». Возникает алгебра чисел – .

2. Задано произвольное множество и операция « * » (или « + »). Получаемая алгебра называется группой.

Частные случаи:

– = , « * » – группа целых чисел.

– (, « + ») – группа целых чисел; (2, « + ») – подгруппа группы целых чисел, или группа четных чисел.

Если функции сигнатуры являются произвольными отношениями, то пара (, ) называется моделью.

Пусть дана алгебра (, ) и подмножество исходных элементов . Применение операции может вывести за пределы этого множества. Замыканием подмножества называется множество, полученное как результат применения всех операций сигнатуры ко всем элементам и к промежуточным результатам применения сигнатуры.

Пример. (2; 4; 10; « + »); 2 + 2 = 4; 2 + 4 = 6 (2; 4; 6; 10; « + ») – все то, что можно получить, и является замыканием (все четные числа).

Элементы сигнатуры называются функторами; – терм. Отображение некоторого множества термов во множество {И, Л} называется атомом. Он состоит из двух объектов: , где – предикат, – список термов.

С введением предикатов алгебра логики приобретает динамику. Аргументы (термы), вообще говоря, пробегают множество значений в некоторой области. Некоторые утверждения высказываются для случаев, когда некоторая переменная (терм) пробегает все множество значений и когда она принимает некоторые значения из допустимых.

Указанием на пункт А или Б являются кванторы: «все» – All: ; «существует» – Exists: .

С помощью кванторов исчисление высказываний обогащается новым типом формул: ; – «И», «Л» в зависимости от .

Переменные, по отношению к которым применим квантор, называются связанными, остальные свободными. В дополнение к этому в исчислении предикатов добавляются новые аксиомы типа

П1 ; П2 ;

MP: :; :.

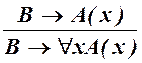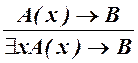Формулой исчисления предикатов является любой стандартный набор, содержащий обычные пропозициональные переменные, снабженные кванторами и , а также связками . Кванторы в этой теории применяются лишь к термам. Такая теория называется теорией первого порядка. В теориях высших порядков кванторы применяются также к литералам – именам пропозициональных переменных и предикатов.

Одной из основных задач является приведение формул исчисления предикатов к виду, удобному для вывода.

Основные идеи такого приведения:

1. .

Пример. Доказать, что число 36 делится на 6. Вместо этого докажем две другие теоремы: 36/2 и 36/3. После доказательства этих теорем следует, что (36/2) и (36/3) (36/6). Значит, исходную формулу желательно представить в виде конъюнкций.

2. Избавиться от отрицаний перед кванторами:

, .

3. .

Пример. Пусть дана плоскость и вектор нормали.

Высказывание 1: все прямые, лежащие в плоскости, перпендикулярны вектору нормали. Высказывание 2: прямая, лежащая в плоскости, перпендикулярна к вектору нормали (квантор – лишний). Значит, надо стремиться оставить только кванторы , после чего их удалить. Для удаления квантора используют рассуждение Сколема.Сам процесс называется сколемизацией:

Алгоритм заключается в выполнении следующих шагов:

Шаг 1. Избавление от импликаций:

Шаг 2. «Протаскивание» отрицаний:

Шаг 3. Вспомогательная операция – разделение связанных переменных. Основная идея заключается в том, что каждая связанная переменная может встречаться только два раза: первый раз – в обозначении квантора, второй – в обозначении терма:

… … (……) = … … (……).

Например, – не имеет смысла; – правильно.

Шаг 4. Приведение к предваренной форме. Основная идея – распространение области действия квантора в наибольшей степени:

Шаг 5. Сколемизация – избавление от квантора . Вместо квантора появляются произвольные функторы.

Шаг 6. Избавление от квантора (согласно аксиоме ).

Шаг 7. Приведение формулы к виду конъюнкции. В результате исходная формула будет представлена в виде конъюнкций предложений. Каждое из предложений может содержать, в свою очередь, дизъюнкции и отрицания.

Шаг 8. Сведение к доказательству предложений – членов конъюнкции. Если каждый из выводов осуществим, то осуществляется вывод всей формулы.

Итак, программирование доказательства теорем сводится к выполнению двух пунктов:

1. Выполнение всех восьми шагов приведения теоремы исчисления предикатов к стандартному виду является работой со стрингами.

2. После осуществления первого пункта теорема приобретает вид конъюнкции нескольких формул, каждая из которых является дизъюнкцией составляющих её предикатов, т.е. имеет вид конъюнкции предложений. Доказательство сводится к выяснению тавтологичности каждого из предложений. Этот процесс поддаётся программированию.

2.4. Приложение исчисления предикатов к аналитической геометрии

С логическими операциями «дизъюнкция» и «конъюнкция» можно сопоставить алгебраические выражения, содержащие операции abs, +, -, /, *.

Операции , – промежуточные:

;

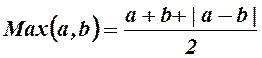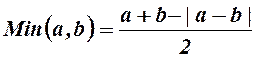Проверка первой формулы:

– пусть , тогда для левой части получим , а для правой – ==;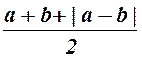

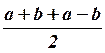– если , то для левой части получим , а для правой – ==.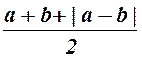

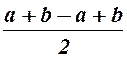Таким образом, имеется возможность с заданной логической функцией, принимающей значение истинности в некоторой области, сопоставить алгебраическую функцию, положительную в этой же области, исходя из уравнений участков границы. Дальнейшее развитие этого подхода заключается в замене модуля функции алгебраическим выражением следующего вида: . Это позволяет представить в аналитическом виде алгебраические эквиваленты дизъюнкции и конъюнкции.

Пусть .

Тогда . Но если каждая из функций положительна, то наименьшая из них также положительна: , или , где .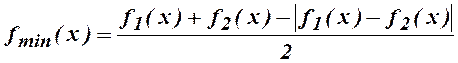

Аналогично вводится функция

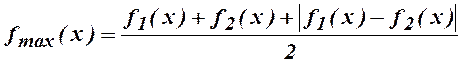Для обеспечения дифференцируемости вводится дополнительное усовершенствование, с помощью которого создаются так называемые R-конъюнкция и R-дизъюнкция:

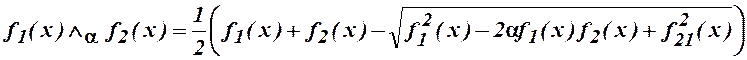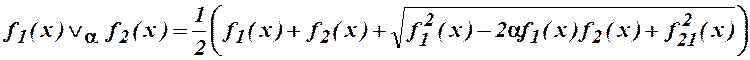Параметр должен удовлетворять неравенству .

С отрицанием сопоставляется предикат следующего вида: если , то .

Пример. Пусть требуется найти аналитическое выражение функции, положительной внутри области, изображенной на рис. 2.1.

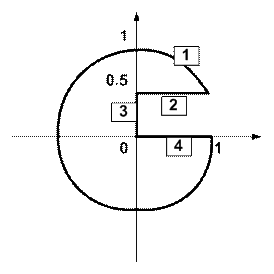
Рис. 2.1. Область, в которой необходимо найти

аналитическое выражение функции

Решение заключается в выполнении нескольких шагов.

1. Запишем уравнения участков границы области:

2. Рассмотрим левую часть круга. В этой части области выполняются неравенства Значение истинности принимает логическая функция следующего вида: , где

Соответствующая R-функция имеет вид

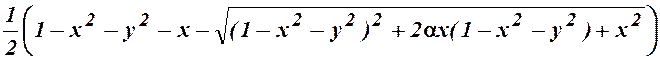3. Рассмотрим верхнюю правую часть области. В этой части области выполняются неравенства . Значение истинности принимает следующая логическая функция:

где .

Последовательно строим соответствующие R-конъюнкции:

4. Аналогично строим R-функцию , которая принимает положительные значения в правой нижней части заданной области.

5. Наконец, R-функция, описывающая область в целом, является R-дизъюнкцией трех найденных R-функций:

Правильность вычислений необходимо проверить. Для этого в прямоугольнике, включающем заданную область, необходимо задать последовательность точек с некоторым шагом по осям Х и Y и в каждой из точек вычислить значение найденной R-функции. Если эта функция в текущей точке положительна, то вывести на экран точку одного цвета, а в противном случае – другого.

Замечание. Построение R-функции неоднозначно. В рассмотренном примере можно было построить R-функцию, положительную внутри области, границами которой являлись бы прямые 2, 3, 4, а затем найти конъюнкцию отрицания найденной функции и функции .

Контрольное задание

В пособии [7, стр. 32-35] выбрать свой вариант и выполнить следующее:

1. Найти уравнения участков границ заданной области, а также соответствующие предикаты, принимающие значение «истина» в заданной области.

2. Построить логическую функцию, истинную в заданной области, используя найденные предикаты. Проверить путем составления программы.

3. Построить аналитическое выражение для функции двух переменных, положительной лишь внутри заданной области. Составить программу для вывода на экран областей уровня полученной функции. Область уровня – множество точек плоскости, для которых выполняется неравенство .