Лабораторная работа №1. Расчет статически неопределимой системы

Цель задания: расчет статически неопределимой системы в условиях работы составляющих ее элементов в режиме растяжения-сжатия (одноосное напряженное состояние).

            Система называется статически неопределимой, если для определения усилий в ее элементах недостаточно уравнений равновесия статики, т.е. число неизвестных внутренних усилий (реакций) больше, чем число уравнений равновесия статики. Степень статической неопределимости системы: К=R-Y, где К- степень статической неопределимости системы; R-число неизвестных внутренних усилий (реакций); Y-число уравнений равновесия статики.

Исходные данные (вариант №3):

            Схема стержневой системы:

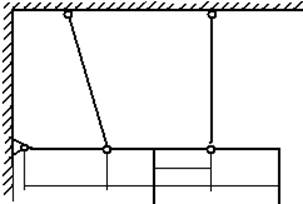
Рис.1

            Материалы стержней: 1-медь, стержень 2-алюминий; упругие модули на растяжение (сжатие): Е₁=МПа; Е₂= МПа; Внешняя сила Р₁=2Н; Р₂=3Н; коэффициенты линейного расширения материалов стержней , . Неточность изготовления элемента системы: стержень 1 изготовлен на величину . Изменение температуры системы . Допустимые напряжения для материалов каждого из стержней:[ ]₁=100 МПа, [ ]₂= 60 МПа.

Конструктивное соотношение площадей стержней F₂/F₁=3 или  F₁/F₂=1/3.

Геометрические размеры: a=2 м, b=1 м, c =0,5 м, d=0,5м, h=1,5м, ,  .

1). Определение усилий от внешней силы Р ().

Вычертим расчетную схему балки с указанием всех размеров. Для расчета усилий используем метод сечений. Сечения проведем через оба стержня. Рассмотрим равновесие нижней части системы, заменяя действие отбрасываемой верхней части стержней внутренними усилиями реакций S₁,S₂.

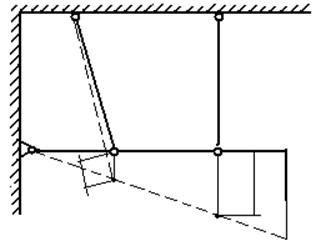
Рис.1

            Составим уравнения статики:

       (2)

или

            .                           (3)

Остальные уравнения статики можно не составлять, так как они необходимы лишь при определении реакций в шарнире X_A,Y_A, чего не требуется по условию задачи. Таким образом, степень статической неопределимости системы К=1, так как мы имеем два неизвестных усилия S₁,S₂ и одно уравнение равновесия статики.

            Для составления одного уравнения совместности деформаций необходимо рассмотреть схему перемещений системы. Под действием внешних сил Р₁ и Р₂ первый стержень удлинится на величину , а второй – на величину , при этом жесткая балка AD повернется в положение AD₁. Ввиду малости упругих деформаций горизонтальными смещениями точек B и C  в ходе деформирования системы переместится строго вертикально и займут положение В₁ и С₁. Положение этих точек определяется пересечением линий AD и перпендикуляров, проведенных к первоначальному направлению осевой линии балки AD в точки В и С.

            Удлинения и  находим также графически, для чего из точек В и С опустим перпендикуляры на линии О₁В₁ и О₂С₁, соответствующие новым положениям стержней 1 и 2 после приложения нагрузки Р. Отрезки В₁В₂ и С₁С₂ определяют удлинения соответственно и .

            Уравнения совместимости деформаций в данном случае проще всего составить, воспользовавшись подобием треугольников АВВ₁ и АСС₁:

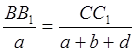                                                           .                                                       (4)

Из треугольников ВВ₁В₂ и СС₁С₂ определим

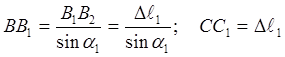                                                 (5)

Подставив равенства (5) в формулу (4), получим уравнение совместности деформаций заданной стержневой системы

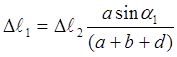                                                                                              (6)

или , где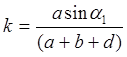

безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы. Используя закон Гука для каждого из стержней

                                   ,

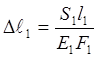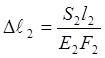
из уравнения (6) получим

                                               .

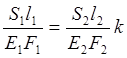Учитывая, что ;  (рис.1), последнее соотношение можно переписать следующим образом:

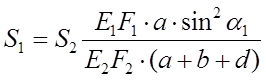                                                                            (7)

Далее решаем совместно систему уравнений (3) и (7):

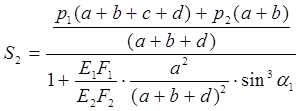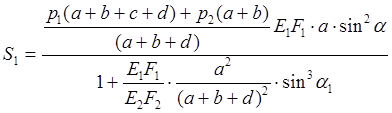;             (8)

Из выражений (8) при известном отношении F₁/F₂ находим численные