




 48. 1-й способ.
Рассмотрим ударное воздействие на систему. Чтобы в составляемые уравнения не
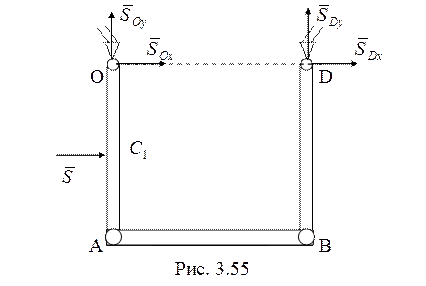
вошли неизвестные ударные импульсы реакций связи в шарнирах О и D (рис. 3.55), воспользуемся теоремой
об изменении кинетической энергии при ударе
48. 1-й способ.
Рассмотрим ударное воздействие на систему. Чтобы в составляемые уравнения не
вошли неизвестные ударные импульсы реакций связи в шарнирах О и D (рис. 3.55), воспользуемся теоремой
об изменении кинетической энергии при ударе
![]() . (3.76)
. (3.76)
Кинетическая энергия
системы ![]() . Для вращающегося стержня ОА
. Для вращающегося стержня ОА ![]() . Для поступательно движущегося стержня АВ
. Для поступательно движущегося стержня АВ ![]() . Для всей системы
. Для всей системы ![]() .
До удара
.
До удара ![]() .
.
Работа ударного импульса 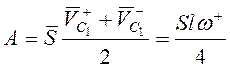 . Тогда из (3.76) следует
. Тогда из (3.76) следует 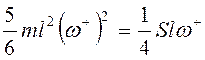 , т.е.
, т.е.
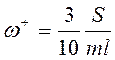 (3.77)
(3.77)
(угловая скорость стержня ОА непосредственно после удара).
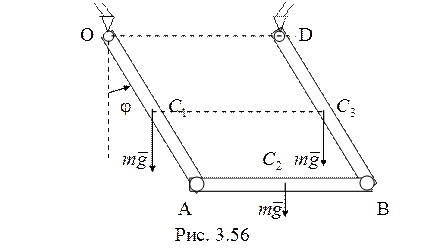
Рассмотрим последующее
движение системы (рис. 3.56). По теореме об изменении кинетической энергии ![]() . Работа сил тяжести
. Работа сил тяжести
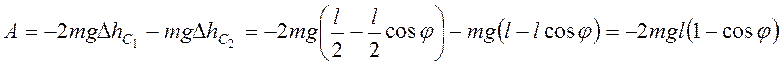 ,
,
 поэтому при максимальном угле отклонения
стержня ОА (так как
поэтому при максимальном угле отклонения
стержня ОА (так как ![]() )
)
![]() .
.
Подстановка (3.77) в последнее выражение
даст 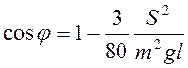 .
.
Максимальный угол отклонения 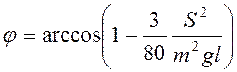 , если
, если 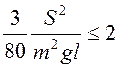 . При
. При 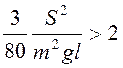 стержень ОА вращается около точки О,
последовательно совершая полные обороты.
стержень ОА вращается около точки О,
последовательно совершая полные обороты.
2-й способ. Возьмем
в качестве обобщенной координаты угол ![]() и воспользуемся уравнением Лагранжа
второго рода при ударе
и воспользуемся уравнением Лагранжа
второго рода при ударе
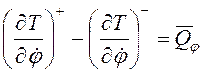 (3.78)
(3.78)
Так как ![]() ,
, 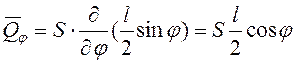 , то из (3.78) следует, что непосредственно после
удара при
, то из (3.78) следует, что непосредственно после
удара при ![]()
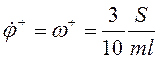 . Далее ход решения из первого способа повторяется.
. Далее ход решения из первого способа повторяется.
Ответ: 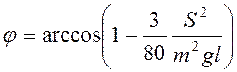 , если
, если ![]() .
.
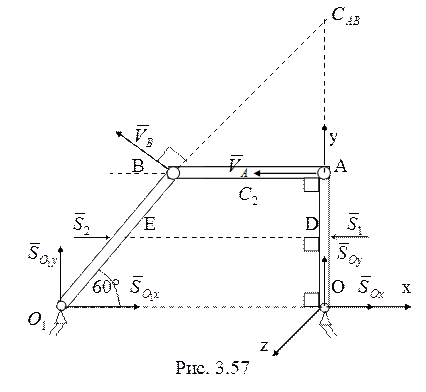
49. Внешние ударные импульсы,
действующие на систему, показаны на рис. 3.57. Чтобы составляемые уравнения не
содержали неизвестных ударных импульсов в шарнирах ![]() и
и ![]() , не совершающих при ударе работу, используем теорему об
изменении кинетической энергии
, не совершающих при ударе работу, используем теорему об
изменении кинетической энергии
![]() . (3.78)
. (3.78)
До удара ![]() . После удара
. После удара ![]() . Для вращающегося стержня
. Для вращающегося стержня ![]() . Момент инерции
. Момент инерции ![]() , и
, и ![]() . Для стержня АВ, приходящего в плоскопараллельное
движение
. Для стержня АВ, приходящего в плоскопараллельное
движение ![]() (точка
(точка ![]() - мгновенный центр скоростей стержня АВ). По теореме
Штейнера
- мгновенный центр скоростей стержня АВ). По теореме
Штейнера 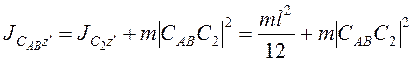 . Так как
. Так как
 |
Угловая скорость 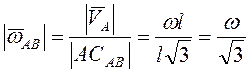 , и кинетическая энергия
, и кинетическая энергия ![]() . Для стержня
. Для стержня ![]()
![]() . Момент инерции
. Момент инерции
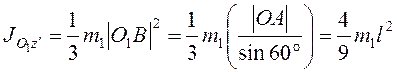 .
.
Угловая скорость 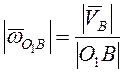 . Из условия недеформируемости стержня АВ
. Из условия недеформируемости стержня АВ
![]() , т.е.
, т.е. ![]() , или
, или 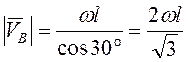 . Тогда
. Тогда ![]() , и
, и
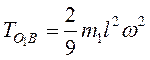 . Для всей системы
. Для всей системы 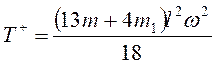 .
.
Работа ударных импульсов
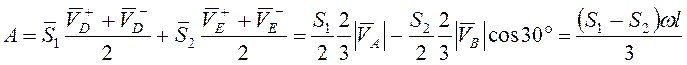 .
.
Из (3.78) следует, что 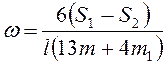 .
.
Ответ: 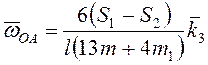 .
.
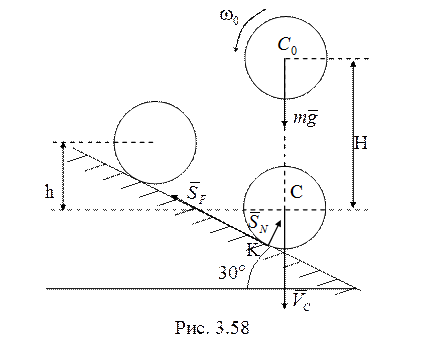 50. Вначале
рассмотрим падение диска (рис. 3.58). По теореме об изменении кинетического
момента относительно центра масс диска
50. Вначале
рассмотрим падение диска (рис. 3.58). По теореме об изменении кинетического
момента относительно центра масс диска 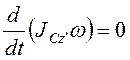 , т.е.
, т.е. ![]() .
.
По теореме об изменении
кинетической энергии ![]() , или
, или
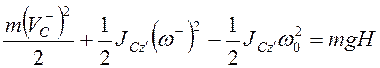 .
.
Отсюда следует, что в момент падения
на наклонную плоскость ![]() .
.
Так как удар является
абсолютно неупругим, то после удара скорость точки соударения К станет равной
нулю. Ударные импульсы ![]() и
и ![]() дают нормальная реакция опоры и сила трения. По
теореме об изменении кинетического момента при ударе относительно оси
дают нормальная реакция опоры и сила трения. По
теореме об изменении кинетического момента при ударе относительно оси ![]() , перпендикулярной плоскости движения диска
, перпендикулярной плоскости движения диска
![]() . (3.79)
. (3.79)
До удара 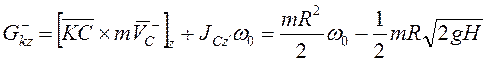 . После удара
. После удара
![]() .
.
Тогда из (3.79) следует, что
непосредственно после удара угловая скорость диска такова, что 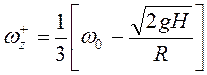 .
.
При подъеме диска по
наклонной плоскости после удара по теореме об изменении кинетической энергии ![]() . Так как
. Так как ![]() ,
, ![]() ,
, ![]() , то
, то 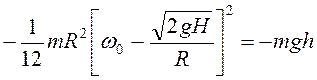 . Отсюда
. Отсюда 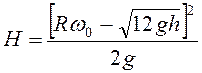 .
.
Ответ: 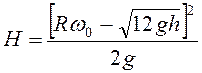
Библиографический список
1. Курс теоретической механики / Под редакцией К.С. Колесникова. М.: Изд–во МГТУ им. Н.Э. Баумана, 2000.
2. Мещерский И.В. Задачи по теоретической механике. С-Пб: Лань, 1998.
3. Пятницкий Е.С., Трухан Н.М., Ханукаев Ю.И., Яковенко Г.Н. Сборник задач по теоретической механике. М.: Наука, 1980.
4. Исмагамбетов М.У., Рощанский В.И. Задачи по основам механики. С-Пб, Изд. центр СПбГМТУ, 1999.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.