Лабораторная работа № 2.
Программирование ветвлений
Цель работы – освоить операции отношения, логические операции, научиться составлять и использовать логические выражения и изучить работу условных операторов.
Постановка задачи
Написать три программы согласно индивидуальному варианту. В первой программе вычислить и вывести значение логического выражения. Во второй программе вычислить значение функции, используя блочный условный оператор. В третьей программе использовать вложенный условный оператор.
Варианты заданий
Вариант 1
1. Выведите на экран значение логического выражения, которое принимает значение true, если Х лежит вне отрезков [2,5] и [-1,1] и false – в противном случае.
2.
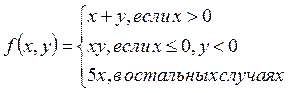
3. Вывести на экран номер четверти, которой принадлежит точка с координатами (x,y), или указать, какой оси принадлежит эта точка.
Вариант 2
1. Покупатель хочет купить игрушку ребенку в возрасте А лет по цене от С1 до С2 рублей. Выведите на экран значение логического выражения, которое принимает значение true, если ему подходит машинка стоимостью 250 руб., предназначенная для детей от 5 до 8 лет, и false – в противном случае.
2.
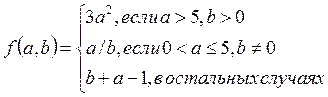
3. Даны 3 целых числа, найти среднее из них. Средним назовем число, которое больше наименьшего и меньше наибольшего.
Вариант 3
1. Даны три целых числа: K, M и N. Выведите на экран значение логического выражения, которое принимает значение true, если среди заданных чисел есть хотя бы два четных и false – в противном случае.
2.
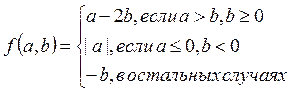
3. Даны стороны треугольника. Определить его вид: равносторонний, равнобедренный или разносторонний - и вывести сообщение об этом. И кроме того, если треугольник равносторонний, то найти его высоту, если он равнобедренный, то найти его полупериметр, а в противном случае найти его наибольшую сторону.
Вариант 4
1. Выведите на экран значение логического выражения, которое принимает значение true, если К является двухзначным числом, кратным пяти и false – в противном случае.
2.
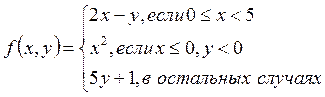
3. Даны два целых числа. Если они оба положительны, то большее из них заменить их средним арифметическим; если оба отрицательны, то поменять знак у меньшего из них; иначе каждое из них удвоить.
Вариант 5
1. Выведите на экран значение логического выражения, которое принимает значение true, если заданное число X лежит вне отрезка [a,b] и является положительным числом, и false – в противном случае.
2.
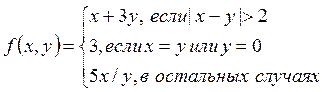
3. Даны два целых числа. Если они оба четны, то большее из них поделить на 2; если оба нечетны, то каждое умножить на 2; в противном случае нечетное из чисел увеличить на 1.
Вариант 6
1. Выведите на экран значение логического выражения, которое принимает значение true, если треугольник со сторонами a, b, c является равнобедренным, и false – в противном случае.
2.
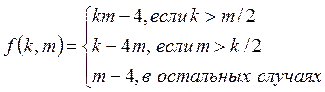
3. Даны 2 числа. Если они оба положительны, то поменять знак у большего из них; если оба отрицательны, то первое умножить на 2, а второе умножить на 3; в противном случае меньшее заменить их полусуммой, а большее уменьшить на 1.
Вариант 7
1. Выведите на экран значение логического выражения, которое принимает значение true, если среди четырёх заданных чисел a, b, c, d наименьшим является а и false – в противном случае.
2.
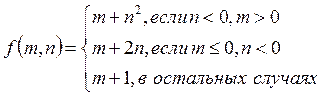
3. Даны координаты двух точек на плоскости. Если хотя бы одна из них лежит на какой-нибудь оси, то вывести сообщение об этом; если они обе находятся в одной четверти, то найти и вывести расстояние между ними; иначе найти точку, наиболее удаленную от центра координат.
Вариант 8
1. Выведите на экран значение логического выражения, которое принимает значение true, если точка с координатами (х,у) принадлежит кольцу с внутренним радиусом R, наружным радиусом R1 и центром в начале координат, и false – в противном случае.
2.
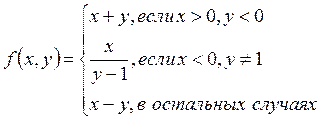
3. Даны 3 целых числа, найти среднее из них. Средним назовем число, которое больше наименьшего и меньше наибольшего.
Вариант 9
1. Выведите на экран значение логического выражения, которое принимает значение true, если заданное натуральное число К является трехзначным числом, кратным трем, и false – в противном случае.
2.
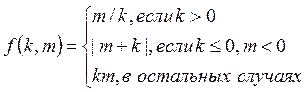
3. Даны три целых числа. Если они все равны, то оставить их без изменения; если они образуют монотонную (т.е. либо возрастающую, либо убывающую) последовательность, то заменить последнее число так, чтобы заданные числа образовали арифметическую прогрессию (считая, что первые два числа являются первыми членами прогрессии); иначе второе число заменить полусуммой первого и третьего чисел.
Вариант 10
1. Выведите на экран значение логического выражения, которое принимает значение true или false в зависимости от того, может ли кирпич, имеющий форму прямоугольного параллелепипеда с ребрами a,b,c, пройти через круглое отверстие с диаметром d.
2.
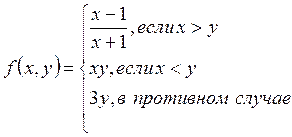
3. Дано натуральное двухзначное число. Если цифры в нем одинаковы, то уменьшить заданное число на 1; если цифры в нем разные, то меньшую из них заменить в заданном числе нулём.
Вариант 11
1. Выведите на экран значение логического выражения, которое принимает значение true, если точка Х на числовой оси попадает в один из двух отрезков [a,b] и [c,d], и false – в противном случае.
2.
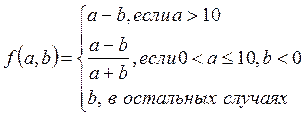
3. Даны 2 числа. Если они оба отрицательны, то первое уменьшить на 1, а второе увеличить на 1; если оба положительны, то большее из них удвоить, а меньшее утроить; в противном случае отрицательное из чисел заменить его абсолютным значением.
Вариант 12
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.