Лабораторная работа № 3. Программирование циклов

Лабораторная работа № 3.
Программирование циклов

Цель работы – научиться различать арифметические и итерационные циклы и реализовывать циклические алгоритмы с помощью операторов цикла со счетчиком(do) и с предусловием( do while).

Постановка задачи

Написать четыре программы согласно индивидуальному варианту. В первом задании запрограммировать арифметический цикл с помощью оператора цикла со счетчиком(do). В задании 2 при написании программы использовать цикл с предусловием(do while). В третьей программе вычислить бесконечную сумму с заданной точностью, используя рекуррентные зависимости. В четвертой - использовать при написании программы конструкцию “цикл в цикле”.

Варианты заданий

Вариант 1   

1.  Получить таблицу температур по Цельсию от 0° до 100° и их эквивалентов по шкале Фаренгейта, используя для перевода формулу .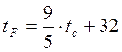

2.  Найти первое число Фибоначчи, большее заданного n (n>1).

3.  Вычислить значение суммы бесконечного ряда с точностью до члена ряда, по модулю меньшего e=10^-4, 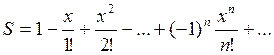, и значение  функции (для проверки) f=e^-x .

4.  Дано целое k>2. Напечатать все простые числа из диапазона [2,k].

Вариант 2   

1.  Вычислить первые 100 чисел Фибоначчи Fn=Fn-1+Fn-2, F0=F1=1.

2.  Пусть последовательность определяется следующим образом x₀=1; x_k=(2-х)/5, k=1,2,…. Найти первый член x_n, для которого .

3.  Вычислить значение суммы бесконечного ряда ,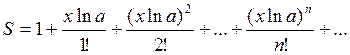
с точностью до члена ряда, меньшего e=10^-4  и значение  функции (для проверки) f=a^x, учесть, что x ограничений не имеет.

4.  Последовательно вводятся вещественные числа. Признаком окончания ввода является отрицательное число или нуль. Вычислить произведение (Х-2)(Х-4)(Х-6)…(Х-22) для каждого из введенных чисел Х.

Вариант 3   

1.  Вычислить F=1!+2!+…+N!

2.  Дано натуральное число N. Составить программу для сравнения цифр старшего и младшего разрядов этого числа.

3.  Вычислить значение суммы бесконечного ряда 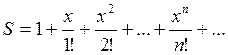 с точностью до члена ряда, по модулю меньшего e=10^-3, и значение  функции (для проверки) f=e^x , учесть, что 1<=x<=2.

4.  Последовательно вводятся числа a, до тех пор, пока не будет введен 0. Для каждого из них вычислить значение функции sinx+a при х, изменяющемся на интервале от –до  с шагом 0.1

Вариант 4   

1.  Пусть дано 20 целых чисел, которые вводятся по одному. Получите сумму тех из них, которые нечетны и отрицательны.

2.  Дано натуральное число N. Составить программу для определения количества цифр в этом числе.

3.  Вычислить значение суммы бесконечного ряда
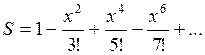, с точностью до члена ряда, по модулю меньшего e=10^-5, и значение  функции (для проверки) f = , учесть, что [-3.14<= x <= 3.14].

4.  Написать программу для поиска 100 первых простых чисел.

Вариант 5   

1.  Вычислить a(a-n)(a-2n)…(a-n²).

2.  Вычислить за сколько лет в банке Сибнефть при начальном вкладе W и процентах годового прироста Pr будет накоплена сумма Sum.

3.  Вычислить значение суммы бесконечного ряда с точностью до члена ряда, по модулю меньшего e=10^-3, 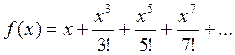, и значение функции (для проверки) .

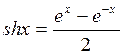4.  Дана последовательность натуральных чисел, за которой следует 0. Вычислить сумму тех из них, порядковые номера которых - простые числа.

Вариант 6   

1.  Последовательно вводятся n действительных чисел. Вычислить среднее арифметическое этих чисел. (Массив не использовать.)

2.  Составить программу для определения, является ли натуральное число k степенью числа 3.

3.  Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-5  s=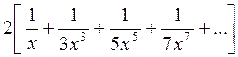 и значение  функции (для проверки) 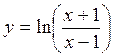, учесть, что [x²>1].

4.  Для каждого из 10 значений переменной Х, изменяющейся от –В до В с постоянным шагом, вычислить значение произведения Р=х*(х+0,2)*(х+0,4)*…*(х+1,8).

Вариант 7   

1.  Вывести таблицу значений функции у=2sinx+cos2x на отрезке от
a=- до b= для значений аргумента x_i=a+ih, i=0,1,2,…n; h=; n=50.

2.  Дано целое m >1. Получить наибольшее целое k, при котором 4^k<m.

3.  Вычислить значение суммы бесконечного ряда 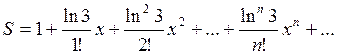, с точностью до члена ряда, по модулю меньшего e=10^-4 , и значение функции (для проверки) f=3^x, учесть, что 0<=x<=1.

4.  Дано К натуральных чисел. Определить сколько из них совершенных. Совершенным называется число, равное сумме всех своих делителей, включая 1 и не включая само число.

Вариант 8   

1.  Последовательно вводятся целые числа х₁,…,х₂₀. Получить сумму тех членов данной последовательности, которые принадлежат заданному интервалу (а,b).

2.  Дано натуральное N. Составить программу для поиска первой цифры этого числа.

3.  Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 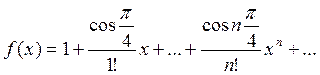, и значение  функции (для проверки) 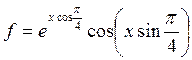, учесть, что  .

4.  Последовательно вводятся целые положительные числа. Для каждого числа выяснить, является ли оно факториалом какого либо числа. Если да, то вывести число, факториалом которого является введенное, если нет, то вывести сообщение об этом. Признаком конца ввода является ввод нуля.

Вариант 9   

1.  Вводится последовательность из N целых чисел. Найти максимальное среди них.

2.  Дано натуральное число N. Выяснить, является ли оно степенью числа 5.

3.  Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 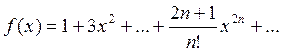, и значение  функции (для проверки) , учесть, что  .

4.  Для каждого из 20 значений переменной Х, изменяющейся от -А до А с постоянным шагом, вычислить значение суммы .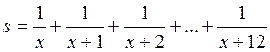

Вариант 10   

1.  Даны натуральное число n и вещественное х. Вычислить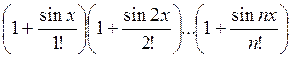

2.  Спортсмен в первый день пробежал10 км. Каждый следующий день он увеличивал дневную норму на 10% от предыдущего дня. Через сколько дней спортсмен будет пробегать в день больше 20 км?

3.  Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 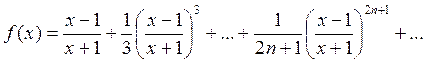, и значение  функции (для проверки) с 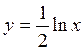, учесть, что  .

4.  Найти натуральное число в диапазоне от 2 до 485 с максимальной суммой делителей (само число в сумму не включать).

Вариант 11   

1.  Даны натуральные числа А и В. Определить все числа, кратные А и В, меньшие А*В.

2.  Факториал некоторого числа равен Р. Найти это число.

3.  Вычислить значение суммы бесконечного ряда 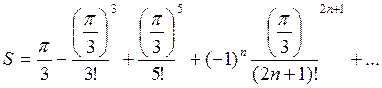с заданной точностью e=10^-4 и  значение функции (для проверки) f=sin.

4.  Для заданных x=2,3,4,5,6,7.8,9,10 вычислить значение y= по рекуррентному соотношению Ньютона: 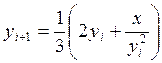, y₀=0.3x. Вычисления продолжать до тех пор, пока не выполнится условие , e=10^-4. Подсчитать сколько итераций надо выполнить для этого.

Вариант 12   

1.  Вычислить и вывести n членов арифметической прогрессии с первым членом а и разностью прогрессии р. Определить их произведение.

2.  Дано действительное а. Вычислить .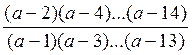

3.  Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 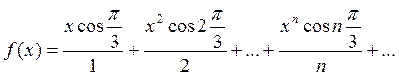, и значение  функции (для проверки)  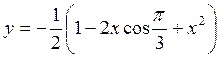учесть, что  .

4.  Дано положительное число С. Для каждого значения х=2,3,4,…,7 найти такое наибольшее целое к, при котором х^к не превышает