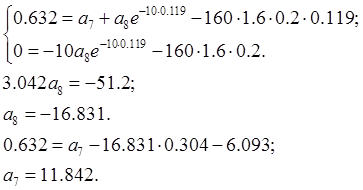
Значит:
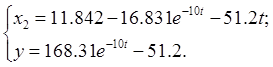 (3.25)
(3.25)
3.5. Решение ![]()
Запишем систему уравнений при данных условиях:
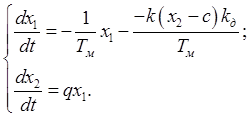
Из второго уравнения
системы находим ![]() и
и ![]() . Затем
полученное выражение подставляем в первое уравнение системы.
. Затем
полученное выражение подставляем в первое уравнение системы.
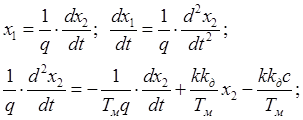
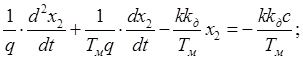 (3.26)
(3.26)
Решение уравнения (3.26) будем искать в виде:
![]()
где ![]() - общее решение уравнения;
- общее решение уравнения;
![]() - частное решение
уравнения.
- частное решение
уравнения.
Найдем ![]() :
:
Запишем характеристическое уравнение:
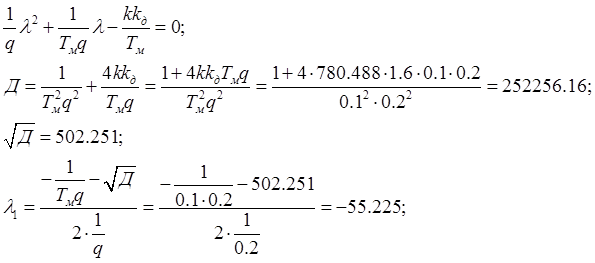
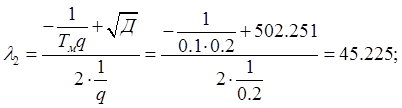
Тогда ![]() будет равно:
будет равно:
![]() (3.27)
(3.27)
Найдем ![]() :
:
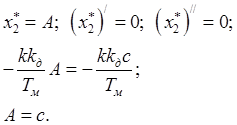
![]() (3.28)
(3.28)
Тогда решение уравнения примет вид:
![]()
![]() (3.29)
(3.29)
![]()
![]() (3.30)
(3.30)
Найдем постоянные ![]() . Начальные условия определим исходя из
того, что
. Начальные условия определим исходя из
того, что ![]() . Тогда из первого уравнения системы (3.25)
находим
. Тогда из первого уравнения системы (3.25)
находим ![]() , использую Maple:
, использую Maple:
> d:=11.842-16.831*exp(-10*t)-51.2*t=0.17;
![]()
> solve(d,t);
![]()
Поскольку ![]() из п. 3.4 равно 0.119, то выбираем что
из п. 3.4 равно 0.119, то выбираем что ![]() Подставляя
Подставляя
![]() во второе уравнение системы (3.25),
получим
во второе уравнение системы (3.25),
получим ![]() :
:
![]()
Тогда:
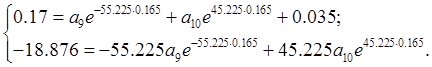
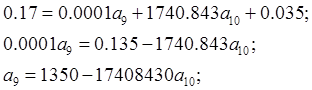
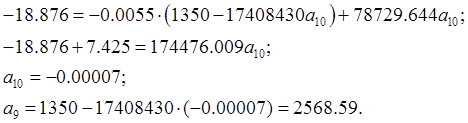
Значит:
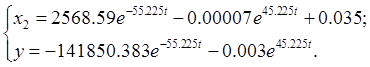 (3.31)
(3.31)
3.6. Решение ![]()
Решение в общем виде находится аналогично п. 3.1. Поэтому можем записать, что
![]() (3.32)
(3.32)
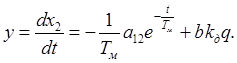 (3.33)
(3.33)
Начальные условия
определим исходя из того, что![]() Тогда из первого
уравнения системы (3.31) находим
Тогда из первого
уравнения системы (3.31) находим ![]() , используя Maple.
, используя Maple.
> d:=2568.59*exp(-55.225*t)-0.00007*exp(45.225*t)+0.035=-0.24;
![]()
> solve(d,t);
0.188
Из второго уравнения
системы (3.31) находим ![]() :
:
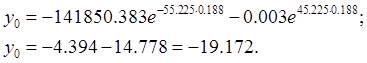
Тогда:
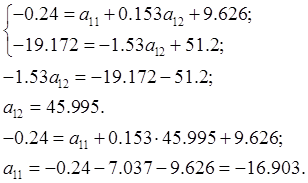
Значит:
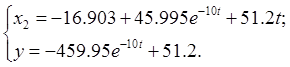 (3.34)
(3.34)
3.7. Решение ![]() .
.
Поскольку ![]() в несколько раз меньше значения
в несколько раз меньше значения ![]() , то при уменьшение
, то при уменьшение ![]() в
несколько раз уменьшаются значения системы уравнения. По аналогии к п. 3.3
можем вычислить разные системы уравнения.
в
несколько раз уменьшаются значения системы уравнения. По аналогии к п. 3.3
можем вычислить разные системы уравнения.
3.8. Решение ![]() .
.
Поскольку ![]() в несколько раз меньше значения
в несколько раз меньше значения ![]() , то при уменьшение
, то при уменьшение ![]() в
несколько раз уменьшаются значения системы уравнения. По аналогии к п. 3.6
можем вычислить разные системы уравнения.
в
несколько раз уменьшаются значения системы уравнения. По аналогии к п. 3.6
можем вычислить разные системы уравнения.
3.9. Построение фазовой траектории.
Построим фазовую траекторию, использую все полученные системы уравнений, которые являются решением системы дифференциальных уравнений на разных интервалах.
При вычислении данных будем использовать язык программирования C++.
Листинг программы приведен в приложении А. Результаты вычислений приведены в приложении Б. График фазовой траектории приведен в приложении В.
3.10. Построение фазового портрета.
Чтобы построить фазовый портрет, необходимо выполнить следующие действия:
· изменить начальные данные в п.3.1;
· провести перерасчет с п.3.1 по п.3.8;
· простроить фазовую траекторию для новых решений;
· построить в одних осях первую и вторую фазовые траектории.
Выполнив эти действия, мы получили фазовый портрет, который изображен в приложении Г.
ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы была исследована автоматическая система следящего электропривода постоянного тока. Функциональная схема этой системы изображена на рис. 1.1. Данная система включала в себя нелинейность типа люфт с зоной насыщения, график которой приведен на рис. 1.2.
Исследование данной системы проводилось методом фазовой плоскости. Этот метод относится к точным методам исследования нелинейных систем. Суть этого метода заключается в построении фазового портрета и анализа его. Фазовый портрет – это совокупность фазовых траекторий , которые соответствуют разным начальным значениям изображающей точки.
Фазовую траекторию данной системы приведено в приложении В, а фазовый портрет – в приложении Г. Глядя на рисунок, можем твердо сказать, что имеет устойчивый граничный цикл. Система находится в режиме автоколебаний. К основным параметрам этого режима можно отнести следующие параметры:
·
амплитуда
автоколебаний ![]() ;
;
·
частота
автоколебаний ![]() ;
;
·
период
автоколебаний ![]() .
.
Определим эти основные параметры:
амплитуда автоколебаний ![]() рад;
рад;
частота автоколебаний 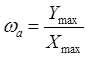
![]()
Тогда 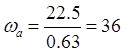 с-1;
с-1;
период автоколебаний 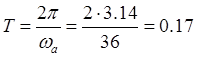 с.
с.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.