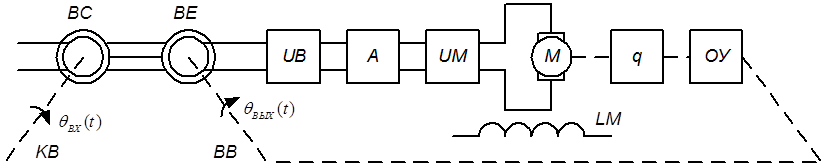
Рис. 1.1 – Функциональная схема электропривода постоянного тока.
После приведения структурной схемы к простейшей считать, что общая нелинейность данной системы является нелинейностью с люфтом и зоной насыщения, график которой изображен на рис. 1.2.
Исходные данные:
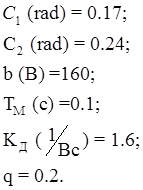
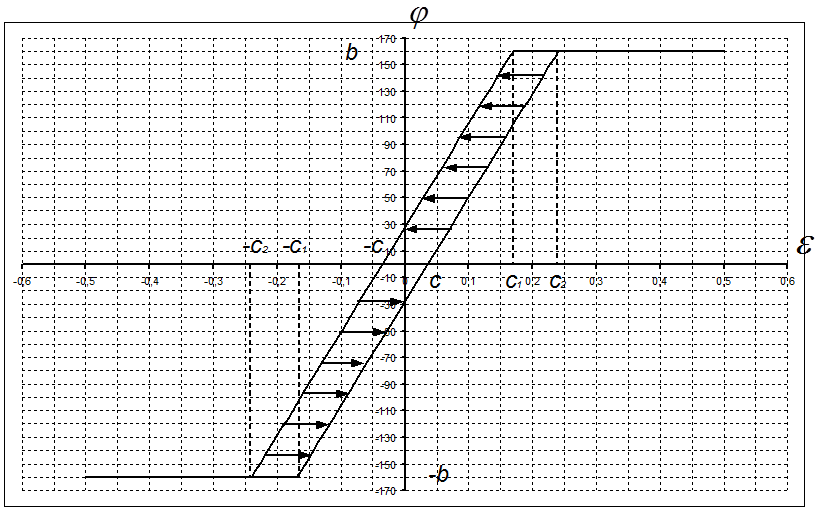
Рис. 1.2 – График нелинейности.
2. МАТАМАТИЧЕСКОЕ ОПИСАНИЕ СЛЕДЯЩЕГО ЭЛЕКТРОПРИВОДА ПОСТОЯННОГО ТОКА
Будем считать, что все элементы электропривода линейные, кроме редуктора, который имеет люфт и зону насыщения. Запишем уравнения линейных элементов электропривода:
· измерительный прибор
![]()
· фазочувствительнный усилитель UB
![]() ;
;
· усилитель напряжения А
![]()
· тиристорнный преобразователь UM
![]()
В этих уравнениях ![]() - коэффициенты передачи
фазочувствительнного выпрямителя, усилителя и тиристорного преобразователя;
- коэффициенты передачи
фазочувствительнного выпрямителя, усилителя и тиристорного преобразователя; ![]() - их выходные напряжения.
- их выходные напряжения.
Двигатель постоянного тока с независимым возбуждением описывается системой уравнений:
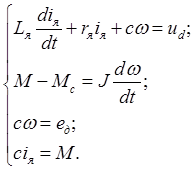 (2.1)
(2.1)
где ![]() - индуктивное и активное сопротивление
якорной цепи;
- индуктивное и активное сопротивление
якорной цепи; ![]() - ток якоря, ЭДС и скорость
двигателя;
- ток якоря, ЭДС и скорость
двигателя; ![]() - коэффициент пропорциональности между ЭДС
и скоростью двигателя, а также между моментом и током якоря при неизменном
потоке возбуждения;
- коэффициент пропорциональности между ЭДС
и скоростью двигателя, а также между моментом и током якоря при неизменном
потоке возбуждения; ![]() - момент статической нагрузки,
приведенный к валу двигателя;
- момент статической нагрузки,
приведенный к валу двигателя; ![]() - суммарный момент
инерции электропривода, приведенный к валу двигателя.
- суммарный момент
инерции электропривода, приведенный к валу двигателя.
Первое уравнение системы (2.1) записано за вторым законом Кирхгофа для цепи якоря, а второе уравнение этой системы – закон равновесия моментов на валу двигателя.
Первое уравнение системы (2.1), учитывая третье уравнение, запишем в таком виде:
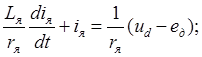 (2.2)
(2.2)
а второе уравнение с учетом четвертого – у виде:
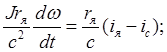 (2.3)
(2.3)
где 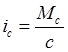 .
.
Введем электромагнитную 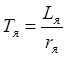 и электромеханическую
и электромеханическую 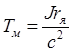 постоянную времени и используем оператор
постоянную времени и используем оператор 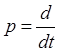 , и запишем уравнения (2.2) и (2.3) у виде:
, и запишем уравнения (2.2) и (2.3) у виде:
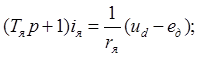 (2.4)
(2.4)
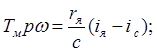 (2.5)
(2.5)
Редуктор с люфтом и зоной насыщения описывается уравнением:
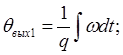 (2.6)
(2.6)
или
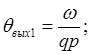 (2.7)
(2.7)
где ![]() - передаточное число редуктора и
уравнениями неоднозначности нелинейной характеристики (2.8).
- передаточное число редуктора и
уравнениями неоднозначности нелинейной характеристики (2.8).
Уравнениям, что описывают элементы следящего электропривода, соответствует структурная схема, на которая изображена на рис. 2.1. Эту схему можно привести к простейшей. Порядок приведения изображено на рис. 2.2, а, б, в. В результате получим схему, которая изображена на рис. 2.3.
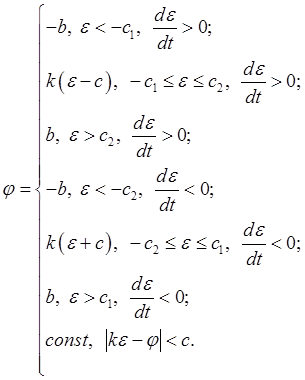 (2.8)
(2.8)
При преобразовании
структурной схемы считается, что ![]() . В этом случае звено,
которое описывает двигатель, заменяется одним звеном с передаточной функцией:
. В этом случае звено,
которое описывает двигатель, заменяется одним звеном с передаточной функцией:
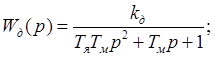 (2.9)
(2.9)
где 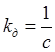 - коэффициент передачи двигателя, и
структурная схема имеет вид, который показан на рис. 2.2, а.
- коэффициент передачи двигателя, и
структурная схема имеет вид, который показан на рис. 2.2, а.
Определивши передаточную функцию линейной части системы:
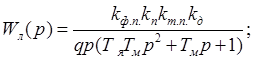 (2.10)
(2.10)
получим структурную
схему, приведенную на рис. 2.2, б. После перенесения сумматора через звено ![]() будем иметь структурную схему, изображенную
на рис. 2.2, в, а после перенесения узла через звено
будем иметь структурную схему, изображенную
на рис. 2.2, в, а после перенесения узла через звено ![]() -
схему на рис. 2.3.
-
схему на рис. 2.3.
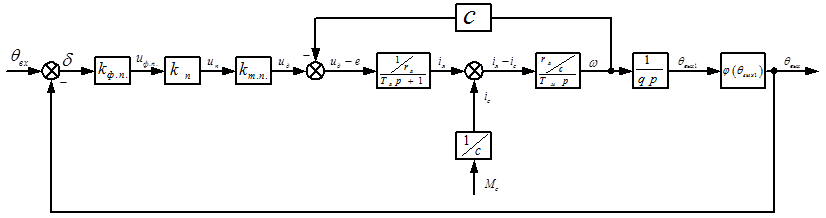
Рис. 2.1 – Исходная структурная схема.
 а)
а)
б)
в)
Рис. 2.2 – Преобразование исходной структурной схемы: а, б, в.

Рис. 2.3 – Преобразованная структурная схема.
3. ИССЛЕДОВАНИЕ СИСТЕМЫ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
Передаточная функция
двигателя описывается формулой 2.9. Допустим, что ![]() . Тогда
передаточная функция двигателя будет иметь вид:
. Тогда
передаточная функция двигателя будет иметь вид:
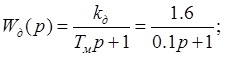 (3.1)
(3.1)
где ![]() - коэффициент передачи двигателя,
- коэффициент передачи двигателя, ![]() - электромеханическая постоянная времени
электропривода.
- электромеханическая постоянная времени
электропривода.
Редуктор, входной
величиной которого есть скорость ![]() , а выходной – угол
поворота
, а выходной – угол
поворота ![]() , описывается передаточной функцией:
, описывается передаточной функцией:
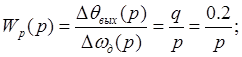 (3.2)
(3.2)
где ![]() - передаточное число редуктора.
- передаточное число редуктора.
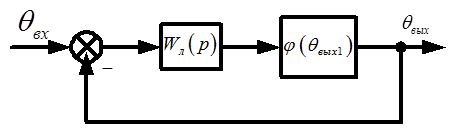
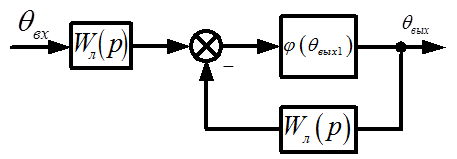
Учитывая формулы 3.1 и 3.2, изобразим структурную схему электропривода (рис. 3.1).
 Рис. 3.1 – Структурная схема электропривода.
Рис. 3.1 – Структурная схема электропривода.
Ее изображено у виде, удобном для математического описания – системой уравнений у нормальной форме Коши:
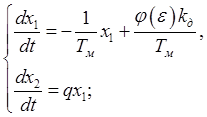 (3.3)
(3.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.