Исследование системы управления с нелинейными объектами, страница 3

Эти уравнения составлены при условии, что , поскольку исследуется свободное движение системы и определить  и .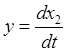

Учитывая что,  перепишем систему уравнений 3.3 относительно :

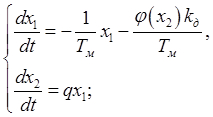                                 (3.4)

Решим данную систему на каждом участке.

3.1. Решение

                                               

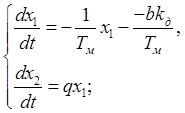
Из второго уравнения системы находим  и . Затем полученное выражение подставляем в первое уравнение системы.

                                       

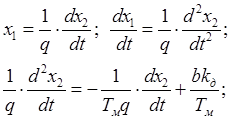
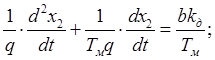                                 (3.5)

Решение уравнения (3.5) будем искать в виде:

где  - общее решение уравнения;

           - частное решение уравнения.

Найдем :

Запишем характеристическое уравнение и найдем его корни:

                                                     

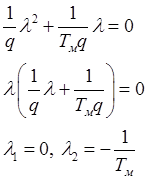
Тогда  будет равно:

                                               (3.6)

Найдем :

                                     

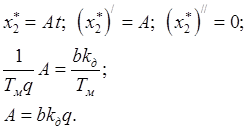
                                                      (3.7)

Тогда решение уравнения примет вид:

                                     (3.8)

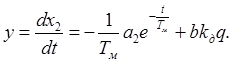                              (3.9)

Найдем постоянные . Зададим начальные условия для первой фазовой траектории:

                                                  

    

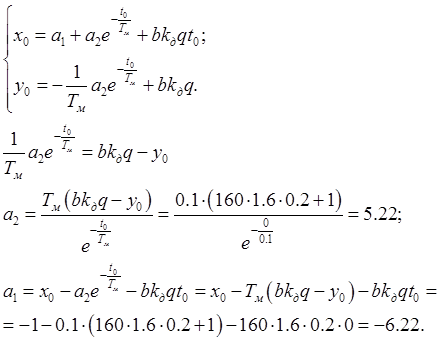
Тогда:

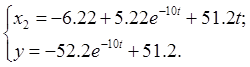                           (3.10)

3.2. Решение

Находим коэффициенты :

                              

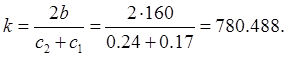
З другой стороны:

                                                               

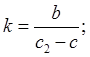
Тогда:

                                 

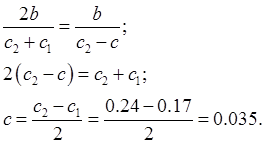
Запишем систему уравнений при данных условиях:

                                    

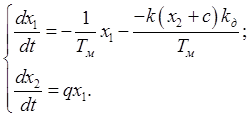
Из второго уравнения системы находим  и . Затем полученное выражение подставляем в первое уравнение системы.

                           

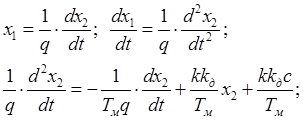
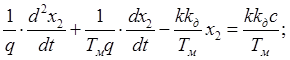                    (3.11)

Решение уравнения (3.11) будем искать в виде:

где  - общее решение уравнения;

           - частное решение уравнения.

Найдем :

Запишем характеристическое уравнение:

           

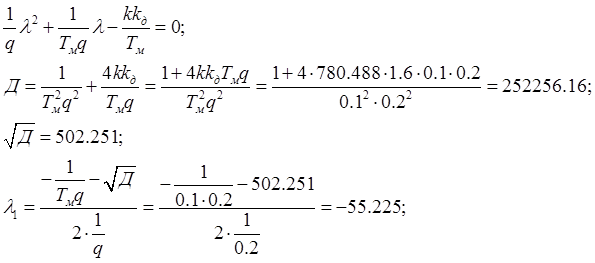
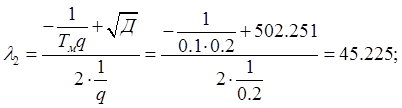
Тогда  будет равно:

                                    (3.12)

Найдем :

                                      

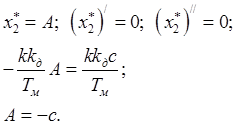
                                                          (3.13)

Тогда решение уравнения примет вид:

                           (3.14)

                   (3.15)

Найдем постоянные . Начальные условия определим исходя из того, что . Тогда из первого уравнения системы (3.10) находим , использую Maple:

> d:=-6.22+5.22*exp(-10*t)+51.2*t=-0.17;

> solve(d,t);

Поскольку время не может быть отрицательным, выбираем  Подставляем  во второе уравнение системы (3.10) и находим

                             

        

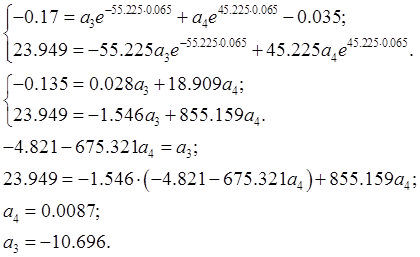
Тогда:

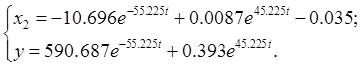        (3.16)

3.3. Решение

                                                 

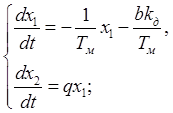
Из второго уравнения системы находим  и . Затем полученное выражение подставляем в первое уравнение системы.

                                       

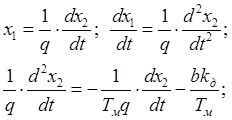
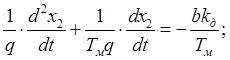                              (3.17)

Решение уравнения (3.6) будем искать в виде:

где  - общее решение уравнения;

           - частное решение уравнения.

Найдем :

Запишем характеристическое уравнение и найдем его корни:

                                                     

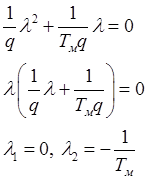
Тогда  будет равно:

                                               (3.18)

Найдем :

                                     

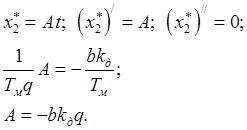
                                                    (3.19)

Тогда решение уравнения примет вид:

                                     (3.20)

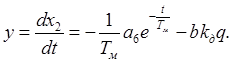                              (3.21)

Найдем постоянные . Начальные условия определим исходя из того, что . Тогда из первого уравнения системы (3.16) находим , использую Maple:

> d:=-10.696*exp(-55.225*t)+0.0087*exp(45.225*t)-0.035=0.24;

> solve(d,t);

0.083

Значит  Подставляя  во второе уравнение системы (3.16), получим :

           

              

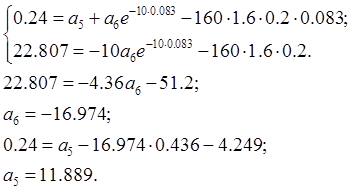
Тогда:

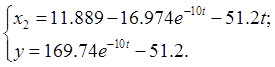                    (3.22)

3.4. Решение

Решение в общем виде находится аналогично п. 3.3. Поэтому можем записать, что

                                     (3.23)

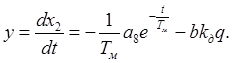                              (3.24)

Начальные условия определим следующим образом: поскольку производная на участке  меняет знак, производная от  равна 0. То есть,  Использую второе уравнение системы (3.22) и Maple, находим время :

> d:=169.74*exp(-10*t)-51.2=0;

> solve(d,t);

Подставляя значение  в первое уравнение системы (3.22), получим:

           

Тогда: