Методичні вказівки до лабораторних робіт з дисципліни “Теорія нелінійних і цифрових систем управління”

Міністерство освіти і науки України

Сумський державний університет

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних робіт з дисципліни

“Теорія нелінійних і цифрових систем управління”

для студентів спеціальності 7.091401

“Системи управління і автоматики”

денної та заочної форм навчання

Суми

Вид-во СумДУ

2006

Кафедра комп’ютеризованих систем управління

Лабораторна робота 1

Дослідження типових нелінійностей

Мета роботи – ознайомитися із системою MATLAB, навчитися будувати графіки перехідних процесів, фазових траєкторій, частотних характеристик, отримати в системі Matlab та дослідити реакцію нелінійних систем на типові сигнали.

1 Теоретичні відомості

Нелінійними САК називаються системи, математичне описання яких не задовольняє умови лінійності. Ці умови полягають у тому, що при зміні зовнішньої дії на ланку або систему в a разів характер перехідного процесу не змінюється, а змінюється лише масштаб вихідної величини у a разів. Крім того, реакція ланки або системи на кілька одночасно прикладених дорівнює сумі реакцій на кожну з цих дій, що прикладені окремо. Якщо САК містить хоча б одну нелінійну ланку, то у цілому вона є нелінійною.

Нелінійні ланки описуються нелінійними рівняннями. Ознакою нелінійних рівнянь є залежність коефіцієнтів рівнянь від координат системи або їх похідних, а також наявність у рівняннях добутків деяких координат чи їх похідних.

Теорію лінійних САК можна застосовувати для аналізу і синтезу реальних систем лише при досить малих відхиленнях від режиму, що досліджується. Проте існує велика кількість САК, у яких нелінійні ланки застосовуються спеціально для забезпечення таких властивостей систем, що принципово не можуть бути досягнуті в лінійних системах. До таких ланок належать релейні елементи і логічні перемикальні пристрої, які дозволяють змінювати структуру САК залежно від деяких її координат, ланки із зоною нечутливості, підсилювачі з насиченням, що забезпечують обмеження координат, тощо.

Задачі аналізу і синтезу нелінійних САК набагато складніші за аналогічні задачі для лінійних систем. Це пояснюється великою різноманітністю та складністю динамічних процесів у нелінійних системах. Стійкість нелінійних систем на відміну  від лінійних залежить від величини і місця прикладання зовнішньої дії, характер перехідного процесу змінюється при зміні величини зовнішньої дії, в нелінійних системах спостерігаються режими, які неможливі в лінійних системах, зокрема режим автоколивань, тощо. Усе це потребує застосування спеціальних точних і наближених методів аналізу і синтезу нелінійних систем.

Типові нелінійності. Нелінійні ланки САК дуже різноманітні. Нелінійні характеристики деяких з них при обмеженому діапазоні зміни вхідного сигналу мало відрізняються від лінійних. Такі нелінійності називають слабкими або несуттєвими. Після лінеаризації цих нелінійностей САК зводять до лінійних і для їх дослідження використовують методи теорії лінійних САК. Іншу групу становлять нелінійні елементи, характеристики яких не можна замінити лінійними. Вони надають САК якісно нових властивостей і, як правило, описуються розривними або близькими до них функціями. Такі нелінійності називають суттєвими.

Характеристики суттєво нелінійних елементів часто ідеалізують, тобто реальну нелінійну характеристику замінюють кількома лінійними ділянками, кожна з яких описується своїм рівнянням. У точках переходу від однієї ділянки до іншої спостерігається розрив похідної, тобто похідна має різні значення при підході до точки розриву зліва і справа. Якщо ідеалізувати суттєво нелінійні характеристики, то їх можна звести до обмеженої кількості типових. Розглянемо найбільш поширені з них. При цьому вважатимемо, що нелінійності безінерційні, тобто не створюють суттєвого запізнення. Такі нелінійності описуються звичайними функціональними залежностями між вхідною і вихідною змінними, які називаються статичними характеристиками  безінерційних нелінійних ланок. У загальному випадку вони мають вигляд

u = j (e),

де u, e – вихідна і вхідна змінні; j – нелінійна функція.

Характеристика із зоною нечутливості. Такі характеристики (рис. 1) мають елементи, в яких вихідний сигнал відсутній при змінюванні вхідного сигналу в деякому інтервалі, звичайно справа і зліва від нуля. Цей інтервал називається зоною нечутливості.

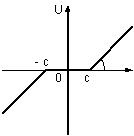
Рисунок 1 – Характеристика із зоною нечутливості

Характеристика на рис.1 кусково-лінійна. Математично кожна лінійна ділянка описується окремо і має вигляд

            k(e+c) при e < – c;

u =       0          при – с £ e £ c;

            k(e–c) при e > c,

де k = tg a.

Зона нечутливості для цієї характеристики становить 2с. За допомогою характеристики із зоною нечутливості можна подати залежність швидкості w двигуна постійного струму з незалежним збудженням від напруги на якорі U_я за умови, що до вала двигуна прикладено реактивний момент статичного навантаження М_с. Зона нечутливості зумовлена тим, що швидкість двигуна дорівнює нулю, якщо його момент М менший за момент статичного навантаження.

Наявність зони нечутливості знижує чутливість системи, тому що система не реагує на сигнали, модуль яких менше с, і часто є небажаною. Але іноді зону нечутливості вводять навмисно, коли необхідно усунути підвищену чутливість системи до перешкод.

Характеристика із зоною насичення. Вигляд цієї характеристики зображено на рис. 2. При малих вхідних сигналах вихідний сигнал пропорційний вхідному, при великих – настає насичення, тобто вихідний сигнал сягає максимального рівня і далі не змінюється.

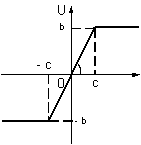
Рисунок 2 – Характеристика із зоною насичення

Математично характеристика описується так:

            – b       при e < – c;

u =       ke       при – с £ e £ c;

             b         при e > c.

Такою характеристикою можна подати залежності вихідної величини від вхідної для більшості типів підсилювачів, тиристорних перетворювачів.

Релейна характеристика. Ця характеристика (рис. 3) відрізняється стрибкоподібним змінюванням вихідного сигналу при переході вхідного сигналу через деякий рівень. Для ідеального реле цей рівень береться таким, що дорівнює нулю, тобто для стрибкоподібного змінювання вихідного сигналу достатньо зміни знака вхідного сигналу.

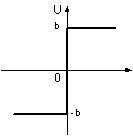
Рисунок 3 – Релейна характеристика

Математично характеристика ідеального реле описується так:

u =         

   b      при e > 0,

або u = b sign e.

Неоднозначні характеристики (характеристики з люфтом, або мертвим ходом). Особливістю цих характеристик є залежність вихідної величини не тільки від вхідної величини в даний момент часу, але й від напрямку її змінювання (зростає вона чи зменшується). Тому при математичному описі таких характеристик використовуються не тільки самі вхідні сигнали