ψba – коэффициент ширины колеса [1, c 17]
b2 = 0,3·130 = 39
округлим до ближайшего стандартного числа, принимаем b2 = 39 мм [1, c 410, табл 24.1]
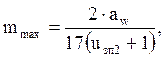
где: mmax – максимальное значение модуля передачи, мм
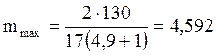
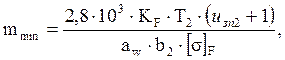
где: mmin – минимальное значение модуля передачи, мм
KF = Kfv·Kfb·Khao,
где: Kfv – коэффициент динамики нагружения [1, c 20, табл 2.9]
Kfb = 0,18+0,82·Khbo,
где: Кfb – коэффициент неравномерности распределения нагрузки
Кfb = 0,18+0,82·1,45 = 1,369
КF = 1,11·1,369·1,5 = 2,279
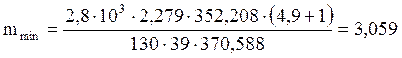
Принимаем m =3мм по стандартному ряду [1,c 21]
Определяем суммарное число зубьев и угол наклона
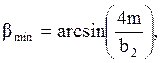
где: βmin – минимальный угол наклона зубьев, ˚
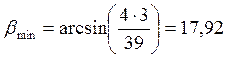
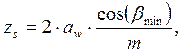
где: zs - суммарное число зубьев
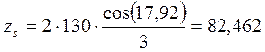
округляем в меньшую строну до ближайшего целого, принимаем zs = 82
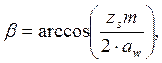
где: β – угол наклона зубьев колеса, ˚
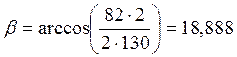
округляем по ряду предпочтительных чисел, принимаем β=19 ˚ [1, c 410, табл 24.1]
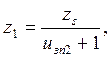
где: z1 – число зубьев шестерни
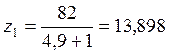
z1 колеса делаем без смещения, принимаем x1=0, x2=0
где: z2 – число зубьев колеса
z2 = 17· 4 = 68
фактическое передаточное число
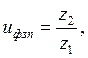
где: uфзп – фактическое передаточное число зубчатой передачи
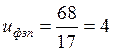
Размеры колёс
где d1 – делительный диаметр шестерни, мм
принимаем d1 = 54мм
d2 = m·z2 , d2 = 3· 68 = 204
где: d2 – делительный диаметр колеса, мм
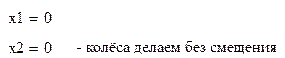
-коэффициент воспринимаемого
смещения
da1 = 54+2(1+0+0)2 = 60
где: da1 – диаметр вершин зубьев шестерни, мм
df1 = 54-2(1,25-0)2= 46,5
где: df1 – диаметр впадин зубьев шестерни, мм
da2 = 204+2(1+0)2 = 210
где: da2 – диаметр вершин зубьев колеса, мм
df2 = 204-2(1,25-0)2= 196,5
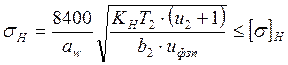
где: σH - расчётные контактные напряжения, МПа
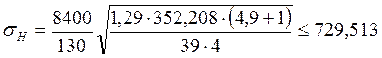
условие выполняется т.е. передача по условию контактной прочности является работоспособной.
Ft=2·103·T2/d1, Ft = 2·103·552,208/54 = 1,305·104
где: Ft – окружная сила, Н
Fr = Ft·0,364/cosβ, Fr = 3,633·103·0,364/сos19= 5,022·103
где: Fr – радиальная сила, Н
Fa = Ft·cosβ, Fa = 3,633·103·cos19 = 4,492·103
;
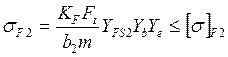где: σF2 – расчётное напряжение изгиба, МПа
[σ]F2 – допускаемые напряжения изгиба, МПа
-
приведенное число зубьев
YFS2 – коэффициент формы зуба, [1, c 24, табл 2.10]
–
коэффициент угла наклона зубьев
Ye – коэффициент перекрытия зубьев, [1, c 24]
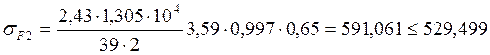
Условие выполняется, т.е. зубья выдержат напряжения изгиба.
;
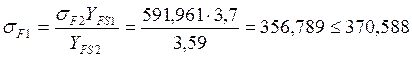где: σF2 – расчётное напряжение изгиба, МПа
-
приведенное число зубьев
YFS1 – коэффициент формы зуба шестерни, [1, c 24, табл 2.10]
Условие выполняется, т.е. зубья выдержат напряжения изгиба.
Выбираем муфту упругую втулочно-пальцевую 250 –32-I.1-45-II.2-У3 ГОСТ 21424-75, так как выходной вал электродвигателя d=45.
dп = d1 +3t = 32+3·3,5 = 39 мм – диаметр под подшипник
где: t – высота заплечика, [1, c 42]
выбираем подшипник роликовый
радиально-упорный с диаметром внутреннего кольца 55 мм и принимаем dп1 = 40мм
dбп = dп1 + 3r = 30+3·2,5 = 47,5 мм – диаметр под колесо
где: r = 2,5 – фаска подшипника [1, c 42]
мм – диаметр
конца вала
принимаем dпр=40 мм
dп = dпр - 2·t = 20-2·3,5= 35мм – диаметр вала под подшипник
где: t – высота заплечика, [1, c 42]
выбираем подшипник роликовый радиально-упорный с диаметром внутреннего кольца 80 мм и принимаем dп1 = 30мм
dбп = dп+3r = 35+3·2,5 = 42,5 мм – диаметр буртика
где: r – фаска подшипника [1, c 42]
dбк = dпр +3f = 40+3·1,2 = 43,6 мм – диаметр буртика
где: f – размер фаски колеса, мм [1, c 42]
Вал 3
dп = d3 + 2·t = 35+2·3,5= 42мм – диаметр вала под подшипник
где: t – высота заплечика, [1, c 42]
выбираем подшипник шариковый радиально однорядный с диаметром внутреннего кольца 100 мм и принимаем dп = 45мм
dбп = dп+3r = 45+3·2,5 = 52,5 мм – диаметр буртика
где: r – фаска подшипника [1, c 42]
- диаметр выходного конца вала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.