где: Khb = 1+(Khbo-1)·Khw,
где: Khbo – коэффициент неравномерности распределения нагрузки в начальный период работы передачи [1, c 19, табл 2.7]
Khw – коэффициент приработки зубьев [1, c 19, табл 2.8]
Khb = 1+(1,07-1)·0,28 = 1,0276
Кhv – коэффициент динамики нагружения [1, c 17, табл 2.6]
Кha = 1+(Khao-1)·Khw,
где: Khao =1+А·(nст-5),
где: Кhao - коэффициент неравномерности распределения нагрузки в начальный период работы передачи
nст – степень точности передачи (принимаем nст =7 исходя из выполнения дальнейшего условия)
Khao = 1+0,25·(7-5) = 1,5 (<1,6)
Kha = 1+(1,5-1)·0,28 = 1,13
KH = 1,02·1,12·1,13 = 1,29
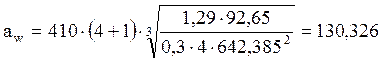
принимаем межосевое расстояние aw = 130 мм, округлив до ближайшего стандартного [1, c 410, табл 24.1]
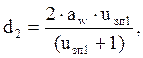
где: d2 – делительный диаметр колеса, мм
aw – межосевое расстояние, мм
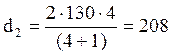
b2 = ψba·aw,
где: b2 – ширина колеса, мм
ψba – коэффициент ширины колеса [1, c 17]
b2 = 0,3·130 = 39
округлим до ближайшего стандартного числа, принимаем b2 = 39 мм [1, c 410, табл 24.1]
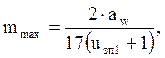
где: mmax – максимальное значение модуля передачи, мм
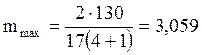
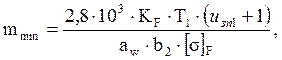
где: mmin – минимальное значение модуля передачи, мм
KF = Kfv·Kfb·Khao,
где: Kfv – коэффициент динамики нагружения [1, c 20, табл 2.9]
Kfb = 0,18+0,82·Khbo,
где: Кfb – коэффициент неравномерности распределения нагрузки
Кfb = 0,18+0,82·1,27 = 1,221
КF = 1,33·1,221·1,5 = 2,43
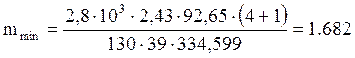
Принимаем m =2мм по стандартному ряду [1,c 21]
Определяем суммарное число зубьев и угол наклона
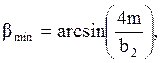
где: βmin – минимальный угол наклона зубьев, ˚
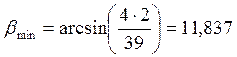
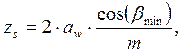
где: zs - суммарное число зубьев
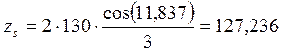
округляем в меньшую строну до ближайшего целого, принимаем zs = 127
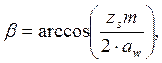
где: β – угол наклона зубьев колеса, ˚
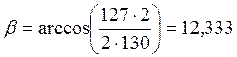
округляем по ряду предпочтительных чисел, принимаем β=12 ˚ [1, c 410, табл 24.1]
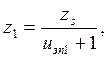
где: z1 – число зубьев шестерни
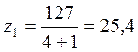
z1 колеса делаем без смещения, принимаем x1=0, x2=0
где: z2 – число зубьев колеса
z2 = 25· 4 = 100
фактическое передаточное число
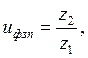
где: uфзп – фактическое передаточное число зубчатой передачи
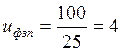
Размеры колёс
где d1 – делительный диаметр шестерни, мм
принимаем d1 = 51мм
d2 = m·z2 , d2 = 2· 100 = 200
где: d2 – делительный диаметр колеса, мм
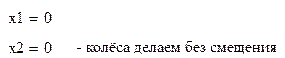
-коэффициент воспринимаемого
смещения
da1 = 51+2(1+0+0)2 = 55
где: da1 – диаметр вершин зубьев шестерни, мм
df1 = 51-2(1,25-0)2= 46
где: df1 – диаметр впадин зубьев шестерни, мм
da2 = 200+2(1+0)2 = 204
где: da2 – диаметр вершин зубьев колеса, мм
df2 = 200-2(1,25-0)2= 195
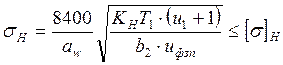
где: σH - расчётные контактные напряжения, МПа
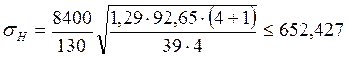
условие выполняется т.е. передача по условию контактной прочности является работоспособной.
Ft=2·103·T1/d1, Ft = 2·103·92,65/51 = 3,633·103
где: Ft – окружная сила, Н
Fr = Ft·0,364/cosβ, Fr = 3,633·103·0,364/сos12 = 1,352·103
где: Fr – радиальная сила, Н
Fa = Ft·cosβ, Fa = 3,633·103·cos12 = 772,266
;
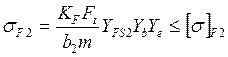где: σF2 – расчётное напряжение изгиба, МПа
[σ]F2 – допускаемые напряжения изгиба, МПа
-
приведенное число зубьев
YFS2 – коэффициент формы зуба, [1, c 24, табл 2.10]
–
коэффициент угла наклона зубьев
Ye – коэффициент перекрытия зубьев, [1, c 24]
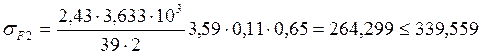
Условие выполняется, т.е. зубья выдержат напряжения изгиба.
;
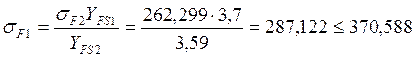где: σF2 – расчётное напряжение изгиба, МПа
-
приведенное число зубьев
YFS1 – коэффициент формы зуба шестерни, [1, c 24, табл 2.10]
Условие выполняется, т.е. зубья выдержат напряжения изгиба.
выбираем материал для шестерни – Сталь 45 (улучшение) HB1 285, σт1 = 650 МПа
колесо – Сталь 45 (улучшение) HB2 250, σт2 = 540 Мпа
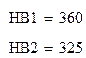
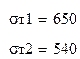
Определяем коэффициенты долговечности для шестерни и колеса
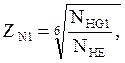(6.1)
где: ZN1 – коэффициент долговечности для шестерни
NHG1 = 30·HB12,4
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.