Планетарные передачи. Кинематический анализ планетарных передач. Синтез планетарных передач, страница 5

4) Условие правильного зацепления – это условие отсутствия заклинивания передачи (при значительном числе зубьев колес, выполненных без подреза ножки и головки зубьев). Чтобы избежать заклинивания зубчатых передач внутреннего зацепления, составленных из эвольвентных нулевых колес с прямыми зубьями необходимо выбирать  каждого колеса передачи больше допускаемого минимального числа зубьев . Для колес с внутренними зубьями при  и коэффициенте высоты головки зуба  имеем , если , то . Для колес с внешними зубьями соответственно имеем  и . Причем для всей передачи разность чисел зубьев сцепляющихся колес () должна быть не менее 8 при  и 7 при .

Во избежание подреза зубьев эвольвентных нулевых колес для передач внешнего зацепления при  и коэффициенте высоты головки зуба  следует выбирать , а при  – .

Заданное передаточное отношение обеспечивается подбором чисел зубьев колес так, чтобы допустимое отклонение фактического передаточного отношения от заданного не превышало 1…4 %.

Существует несколько методов подбора чисел зубьев. Наиболее распространенным является метод сомножителей, при котором числа зубьев определяются только по двум условиям – передаточному отношению и условию соосности, а проверка полученных чисел зубьев – по условиям сборки и соседства. Суть метода сомножителей рассмотрим на примере планетарного механизма, выполненного по схеме (см. табл. 10.1, графа 4), с нулевыми колесами. Из уравнения передаточного отношения этой схемы

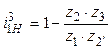
находим значение дроби

.

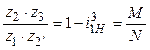Каждое из двух взаимно простых чисел M и N несократимой дроби представляем в идее сомножителей

.

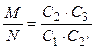В свою очередь, каждое из простых чисел  должно быть пропорционально соответствующему числу зубьев . Тогда условие соосности (см. табл. 10.1) можно представить в виде

.                                                (10.7)

Умножим левую часть тождества на , а правую часть – на :

.

Раскрывая скобки, получим

.

Из последнего тождества следует, что числа зубьев колес будут определяться по следующим выражениям

;          ;

;          ,

uде q – любое положительное целое число, вводимое для обеспечения условия правильного зацепления.

Аналогично определяются числа зубьев колес для других схем планетарных механизмов (см. табл. 10.1).

Пример 10.1. Требуется подобрать числа зубьев колес планетарной передачи, выполненной по схеме (см. табл. 10.1, графа 3), у которой передаточное отношение .

Решение.

1) Из уравнения передаточного отношения имеем

.

Раскладываем число 12 на сомножители:

.

По формулам, приведенным в табл. 10.1, графа 3, получаем три варианта чисел зубьев колес. Расчет чисел зубьев колес сведен в таблицу 10.2

По условию правильного зацепления для первого варианта выбираем , для второго варианта – , для третьего варианта – . Наименьшие габариты механизма будут у второго варианта, который далее проверяем по другим условиям.

Таблица 10.2. Варианты чисел зубьев колес

Число зубьев	Вариант 1	Вариант 2	Вариант 3

2) Проверяем выбранный вариант по условию сборки:

.

Выражение  дает целое число, следовательно, при сборке не требуется дополнительного числа полных оборотов водила . В этом случае для установки второго сателлита потребуется повернуть водило только на угол

.

3) Условие соседства сателлитов проверяем по неравенству

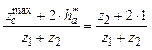 > ;      > ;     0,866 > 0,689.

Так как выполнены все условия, принимаем , , , .

Коэффициент полезного действия планетарных передач определяется по следующим формулам

;       ,

где  – коэффициент потерь обращенного механизма;  – КПД обращенного механизма.

Для схем планетарных передач, приведенных в табл. 10.1, КПД обращенного механизма равен:

,

где  – КПД зубчатого зацепления.

В табл. 10.1 приведены в окончательном виде формулы для определения КПД планетарных передач при различных ведущем и неподвижном звеньях.