Планетарные передачи. Кинематический анализ планетарных передач. Синтез планетарных передач, страница 2

Таким образом, заданное передаточное отношение можно обеспечить множеством различных схем планетарных передач, которые будут значительно отличаться по размерам, КПД, динамическим качествам.

10.2. Кинематический анализ планетарных передач

Основной характеристикой планетарной передачи является передаточное отношение i. Передаточное отношение может быть выражено через отношение чисел зубьев (z), угловых скоростей (ω), частот вращения (n). Существуют аналитический и графический методы кинематического исследования передачи.

10.2.1. Аналитический метод анализа

Пусть требуется определить передаточное отношение  от центрального колеса 1 к водилу Н при неподвижном центральном колесе 3 для планетарного механизма, изображенного на рис. 10.6, а, б.

Рис. 10.6. Планетарный (а, б) и обращенный (в) механизмы:

1 – ведущее центральное колесо; 2 – сателлит; 3 – неподвижное

центральное колесо; Н – водило

Аналитический метод (метод инверсии) определения передаточного отношения основан на принципе обращения движения, который впервые предложен Виллисом. Суть метода заключается в следующем: всему механизму придается угловая скорость , в результате чего водило Н останавливается, а колесо 3 начинает вращаться с угловой скоростью . Звенья обращенного механизма будут вращаться с угловыми скоростями

;       ;       ,

где , ,  – угловые скорости, соответственно, звеньев 1, 2 и 3 при остановленном водиле Н (надстрочный индекс указывает на условную неподвижность соответствующего звена).

Определим передаточное отношение  обращенного механизма (рис. 10.6, в) при ведущем звене 1 и выходном звене 3:

,

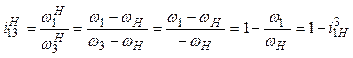откуда найдем передаточное отношение рассматриваемого планетарного механизма

.                                                        (10.1)

При ведущем центральном колесе 3 и неподвижном центральном колесе 1 передаточное отношение планетарного механизма определяется по аналогичной формуле

.                                                        (10.2)

Формулы (10.1) и (10.2) используется для определения передаточного отношения планетарных механизмов при ведущем центральном колесе и выходном водиле Н. При ведущем водиле Н формулы (10.1) и (10.2) приводятся к виду

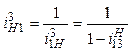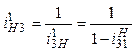;    .                              (10.3)

Теперь определим передаточные отношения рассматриваемого планетарного механизма через числа зубьев колес :

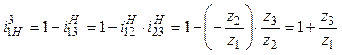;                       (10.4)

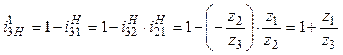;                       (10.5)

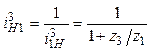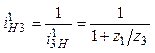;        .                      (10.6)

При определении передаточного отношения планетарного механизма необходимо помнить, что при внешнем зацеплении (зубчатые колеса 1 и 2) знак передаточного отношения отрицательный (так как зубчатые колеса 1 и 2 вращаются в противоположных направлениях), при внутреннем зацеплении (зубчатые колеса 2 и 3) – положительный (зубчатые колеса вращаются в одинаковом направлении).

Пользуясь формулами (10.1) – (10.6), можно аналитически определить угловую скорость любого звена механизма. Найдем, например, угловую скорость  сателлита 2. Для этого составим передаточное отношение:

,

откуда имеем

.

Для других простейших схем планетарных механизмов передаточные отношения приведены в табл. 10.1.

10.2.2. Графический метод анализа

Графический метод определения передаточного отношения планетарного механизма основан на принципе построения линейных скоростей каждого зубчатого колеса, для чего необходимо знать скорости двух его точек. Впервые метод был предложен Л.П. Смирновым и называется методом картин скоростей. Данный метод прост, нагляден и вполне пригоден для большинства инженерных расчетов.

Таблица 10.1. К синтезу планетарных механизмов