Планетарные передачи. Кинематический анализ планетарных передач. Синтез планетарных передач, страница 3

Определим передаточное отношение двухрядного планетарного механизма (рис. 10.7, а) с одним внешним (колеса 1 и 2) и одним внутренним (колеса 2' и 3) зацеплениями, построив план линейных скоростей механизма. Исходными данными являются числа зубьев колес, угловая скорость ведущего звена  и модуль зацепления m (принимаем его одинаковым для внутреннего и внешнего зацеплений). Определяем радиусы делительных окружностей зубчатых колес , полагая колеса нулевыми, по формуле:

.

В масштабе  вычерчиваем схему механизма, который определяется по формуле

,

где  – масштабный коэффициент, м/мм;  радиус делительной окружности зубчатого колеса 1, м; ОА – отрезок на чертеже, изображающий радиус делительной окружности зубчатого колеса 1, мм.

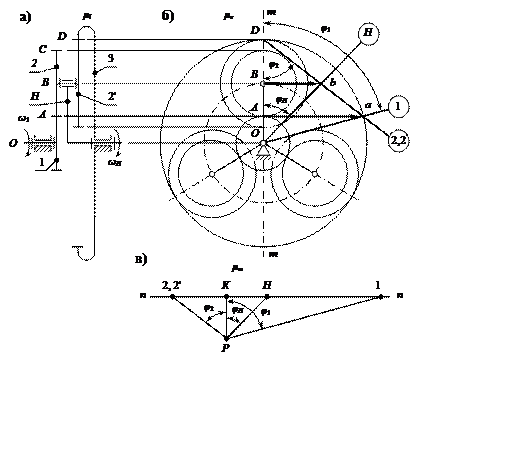
Рис. 10.7. Планетарный двухрядный механизм (а) план линейных (б)

и угловых (в) скоростей

Справа от схемы механизма проводим вертикальную линию т-т (рис. 10.7, б) и проектируем на нее характерные точки: О – ось вращения колеса 1 и водила Н; А и D – зацеплений колес 1, 2 и 2', 3, В – ось вращения блока сателлитов 2 и 2'. Строим план линейных скоростей механизма, начиная с ведущего звена 1, так как для него известны  и .

Определяем скорость точки А зубчатого колеса 1, м/с:

.

Из точки А по горизонтали откладываем отрезок Аа произвольной длины (30…50 мм), изображающий на плане скоростей скорость . Определяем масштабный коэффициент , (м/с)/мм, плана скоростей:

.

Скорость  оси вращения колеса 1 равна нулю, поэтому, соединив точку а с точкой О, получим треугольник скоростей ОАа колеса 1 (или картину распределения скоростей).

Для блока сателлитов 2 и 2' известны линейные скорости точек А и D: в полюсе зацепления колес 1 и 2 линейные скорости их одинаковы, скорость точки D равна нулю, так как данная точка принадлежит также неподвижному колесу 3. Соединив точку а с точкой D, получим треугольник скоростей АDа блока сателлитов 2 и 2'.

Проведя из точки В горизонтальную линию до пересечения с линией DA закона распределения скоростей блока сателлитов 2 и 2', определим скорость точки В (оси вращения сателлитов), предварительно замерив на плане скоростей отрезок Bb:

.

Точка В также принадлежит водилу Н, для которого известна также скорость точки О, значение которой равно нулю, так как ось вращения водила неподвижна. Соединяя точку b с точкой О, получим закон распределения скоростей для водила Н.