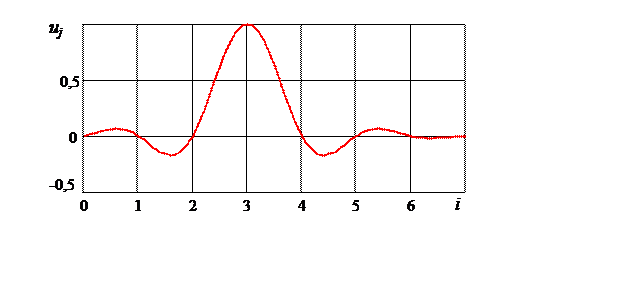
Рис. 4.15. Первичный сигнальный элемент (4.4.1)
с коэффициентом ската ![]()
В этом случае первичные сигнальные элементы формируют
в виде дуобинарных сигнальных импульсов ![]() (рис. 4.16)
(рис. 4.16)
|
|
(4.4.2) |
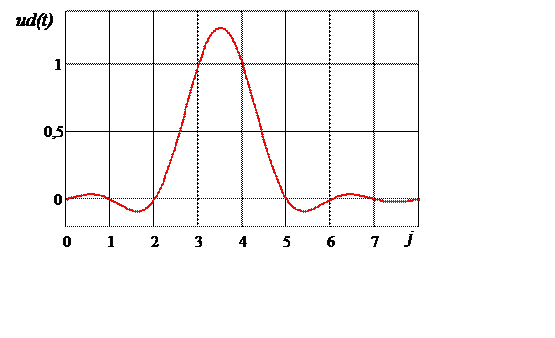
Рис. 4.16. Дуобинарный сигнальный импульс
Дуобинарный сигнальный импульс ![]() имеет
спектр (рис. 4.17)
имеет
спектр (рис. 4.17)
|
|
(4.4.3) |
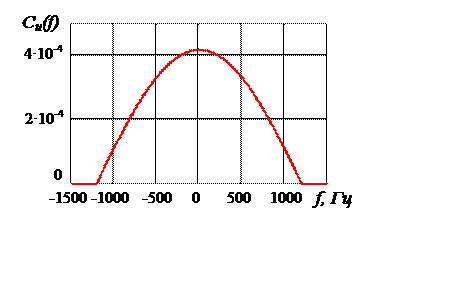
Рис. 4.17. Спектр дуобинарного сигнального импульса при F= 1 200 Гц
Информационный сигнал, сформированный из дуобинарных
сигнальных импульсов ![]() , передаваемых последовательно
друг за другом с частотой следования импульсов Котельникова (Найквиста)
, передаваемых последовательно
друг за другом с частотой следования импульсов Котельникова (Найквиста)
|
|
(4.4.4) |
обеспечивает
контролируемую МСИ в отсчетных точках ![]() (рис. 4.18).
(рис. 4.18).
Таким образом, при передаче информации с помощью двухпозиционного сигнала, образованного дуобинарными сигнальными импульсами, обеспечивают увеличение скорости следования импульсов в два раза по сравнению со скоростью следования первичных сигнальных элементов (4.4.1). Из рисунков 4.6 и 4.18 видно, что это достигается за счет увеличения максимальной амплитуды формируемого сигнала в два раза.
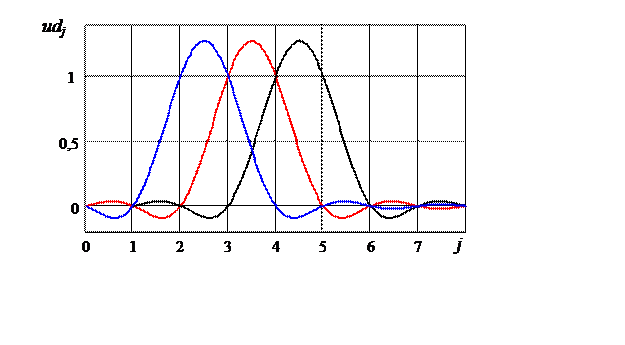
Рис. 4.18. Межсимвольная интерференция
дуобинарных сигнальных импульсов
Еще больший выигрыш можно получить, если с шагом ![]() передать СКК, образованную двумя
двумерными дуобинарными сигнальными импульсами. В этом случае достигается
скорость передачи
передать СКК, образованную двумя
двумерными дуобинарными сигнальными импульсами. В этом случае достигается
скорость передачи ![]() (бит/с). При использовании первичных
сигнальных элементов (4.4.1) такую скорость достигают при передаче информации с
помощью многопозиционного сигнала КАМ-16, который имеет максимальную амплитуду,
превышающую амплитуду первичных сигнальных элементов (4.4.1) в
(бит/с). При использовании первичных
сигнальных элементов (4.4.1) такую скорость достигают при передаче информации с
помощью многопозиционного сигнала КАМ-16, который имеет максимальную амплитуду,
превышающую амплитуду первичных сигнальных элементов (4.4.1) в ![]() раза.
раза.
В процессе приема переданного сообщения осуществляют синхронизацию модемов приемника и передатчика, а также выпол-няют с помощью известных алгоритмов идентификацию матема-тической модели канала связи (например с помощью рекуррентного метода наименьших квадратов), демодуляцию и декодирование принятого многомерного сигнала СКК (например с помощью рекуррентного фильтра Калмана и алгоритма Витерби с мягким решением).
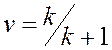 ,
базовая система реализует скорость передачи [71]
,
базовая система реализует скорость передачи [71]|
|
(4.4.5) |
с частотной эффективностью (бит/символ)
|
|
(4.4.6) |
где
![]() - шаг следования
первичных сигнальных элементов.
- шаг следования
первичных сигнальных элементов.
Из формулы (4.4.6) следует, что частотная
эффективность передачи при достаточно большом числе m(при ![]() ) слабо зависит от числа n
составляющих многомерного сигнала и незначительно отличается от своего
предельного значения
) слабо зависит от числа n
составляющих многомерного сигнала и незначительно отличается от своего
предельного значения ![]() . Дальнейшее увеличение частотной
эффективности можно обеспечить лишь за счет увеличения числа mпозиций
сигнального ансамбля СКК. Однако это приводит (при сохранении первоначальной
мощности передатчика) к увеличению вероятности появления ошибок демодуляции,
особенно при использовании нестационарного канала связи с низким отношением
сигнал/шум. Кроме того, описанный традиционный способ передачи сигналов по
каналам связи не обеспечивает конфиденциальности передаваемой информации. Это
связано с тем, что СКК в модеме передатчика формируют из одинаковых первичных
сигнальных элементов
. Дальнейшее увеличение частотной
эффективности можно обеспечить лишь за счет увеличения числа mпозиций
сигнального ансамбля СКК. Однако это приводит (при сохранении первоначальной
мощности передатчика) к увеличению вероятности появления ошибок демодуляции,
особенно при использовании нестационарного канала связи с низким отношением
сигнал/шум. Кроме того, описанный традиционный способ передачи сигналов по
каналам связи не обеспечивает конфиденциальности передаваемой информации. Это
связано с тем, что СКК в модеме передатчика формируют из одинаковых первичных
сигнальных элементов ![]() , которые передают в канал связи
последовательно друг за другом (j = 1, 2, … , N)
с постоянным шагом
, которые передают в канал связи
последовательно друг за другом (j = 1, 2, … , N)
с постоянным шагом ![]() (рис. 4.6). Поэтому
выходной сигнал
(рис. 4.6). Поэтому
выходной сигнал ![]() модема передатчика при передаче
первичного сигнального элемента в моменты времени
модема передатчика при передаче
первичного сигнального элемента в моменты времени
|
|
связан
с амплитудами ![]() синфазной и квадратурной составляю-щих
сигнала линейным уравнением
синфазной и квадратурной составляю-щих
сигнала линейным уравнением
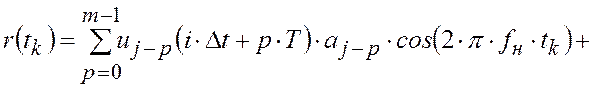
|
|
(4.4.7) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.