Другие предметы \ Автоматизированная система управления технологическим процессом

Синтез адаптивной системы демодуляции КАМ‑сигналов, страница 4

по которой передают импульсы эхосигнала

Адаптивный приемник содержит систему идентификации математической модели канала связи, которая реализует алгоритм (4.2.6), (4.2.8)-(4.2.12).

С помощью этой системы выполнено имитационное моделирование процесса идентификации математической модели канала связи с использованием разработанного способа в условиях МСИ. Уровень суммарного аддитивного шума составлял 15–5 дБ. Идентификация вектора параметров модели канала связи осуществлялась в процессе передачи модемами абонентов последовательности служебных (настроечных) символов, известной на приемной стороне. Число служебных импульсов, используемых для идентификации импульсной функции канала связи, изменяли в диапазоне от 200 до 2 000.

На рисунке 4.7 приведен сигнал, принятый модемом приемника при величине отношения сигнал/эхосигнал равном 5 дБ. Кроме того, на этом же рисунке показан эхосигнал, содержащийся в принятом суммарном сигнале.

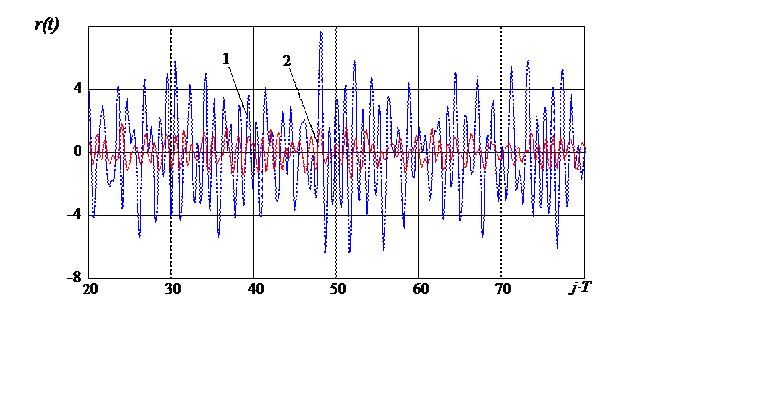
Рис. 4.7. Сигнал, принятый модемом приемника (1), и эхосигнал (2)

Результаты идентификации импульсной функции модели канала связи по алгоритму (4.1.10), (4.1.12)-(4.1.16) с использованием этого сообщения, содержащего 600 символов, представлены на рисунке 4.8. На рисунке 4.8 изображены действительная импульсная функция канала радиоперехвата (линия 1) и ее оценка (линия 2), вычисленная по алгоритму (4.2.6), (4.2.8)-(4.2.12). Здесь же приведена оценка этой импульсной функции (линия 3), вычисленная по той же самой выборке с помощью рекуррентного МНК (по алгоритму фильтра Калмана).

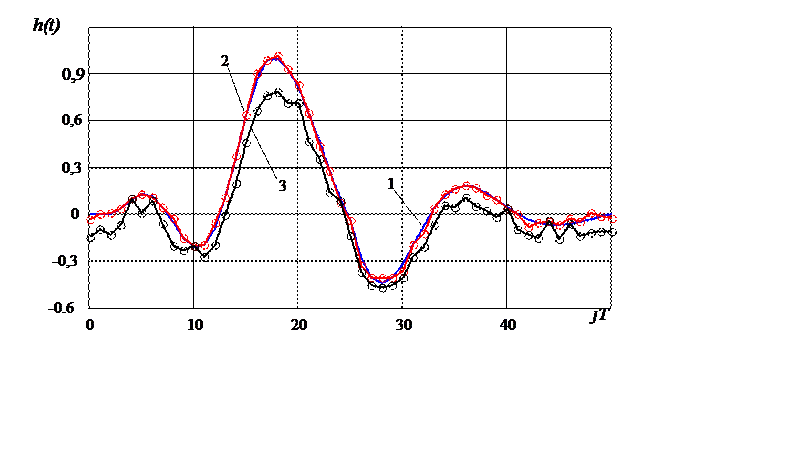
Рис. 4.8. Результаты идентификации импульсной функции канала связи при отношении сигнал/эхосигнал 5дБ:

1 – импульсная функция канала связи; 2 – оценка импульсной функции, вычисленная по алгоритму (4.1.10), (4.1.12)-(4.1.16); 3 – оценка импульсной функции, вычисленная по алгоритму фильтра Калмана

Из рисунка 4.8 видно, что алгоритм (4.2.6), (4.2.8) - (4.2.12) обеспечивает точность идентификации импульсной функции, достаточную для качественной демодуляции принятого сообщения. При этом разработанный алгоритм обеспечивает более высокую точность идентификации параметров модели канала связи по сравнению с алгоритмом фильтра Калмана при использовании одной и той же выборки. Среднюю погрешность идентификации импульсной функции, равную 0,5 %, разработанный алгоритм обеспечивает при использовании выборки, полученной при передаче по каналу связи 400 служебных импульсов при величине отношения сигнал/эхо-сигнал 7 децибел. Уровень суммарного аддитивного шума составлял 5 децибел. С помощью фильтра Калмана эта погрешность идентификации импульсной функции была достигнута при использовании информации, содержащейся в выборке, полученной при передаче 1500 служебных импульсов. Аналогичные результаты были получены и для других комбинаций информационного сигнала, эхо-сигнала и гауссовского шума при передаче по каналу связи КАМ-сигналов.

Таким образом, в разделе 4.2 разработан алгоритм идентификации математической модели канала связи многопозиционных КАМ-сигналов, который не требует знания функций распределения вероятностей шумов. Этот алгоритм обеспечивает минимальную величину обобщенного показателя эффективности (4.1.11), который представляет собой аддитивную свертку сигнала рассогласования, скользящего среднего по времени сигнала рассогласования и среднего по времени квадрата отклонения текущих значений сигналов рассогласования от своих скользящих средних значений, вычисленных в скользящем временном окне.

4.3. Адаптивная система демодуляции КАМ-сигналов,

принятых по каналу связи с неизвестной математической моделью

Для вывода алгоритма демодуляции КАМ-сигналов преобразуем математическую модель канала связи (4.1.1) - (4.1.3) следующим образом.

В скользящем временном окне с номером , которое имеет величину