The common situation, an operator Yt of the complicated algorithm (describing, for example, the functioning of the automated management system) depends on finite subset of logic conditions {xi1,…,xir} out of the total logic conditions set X.
In this connection, it is convenient to use the specialized language for algorithms determining.
An elementary sequence determines the condition to execute the following operator Yj after the operator Yi. A sequence is represented in a form (28.1):
![]() (28.1)
(28.1)
The
symbol ![]() means “if then”. The formula (28.1)
is to be read in such the way: the operator Yj will be executed
after the operator Yi if the condition
means “if then”. The formula (28.1)
is to be read in such the way: the operator Yj will be executed
after the operator Yi if the condition ![]() holds
true.
holds
true.
If the operator Yj has many operators- predecessors, the sequence is represented in the generalized form the system of sequences:
![]() , j=1,…,T. (28.2)
, j=1,…,T. (28.2)
An example of algorithm representation in a form of the system of sequences:
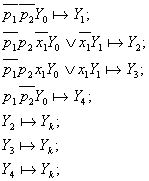 (28.3)
(28.3)
It is easy to obtain the MSA right out of the system of sequences (the table 28.1).
The sequence representation of an algorithm has advantage of compactness. Further, having obtained the MSA, the system of transition formulas may be written down.
Table 28.1
|
MSA |
Y1 |
Y2 |
Y3 |
Y4 |
YT |
|
Y0 |
|
|
|
|
|
|
Y1 |
|
|
|||
|
Y2 |
1 |
||||
|
Y3 |
1 |
||||
|
Y4 |
1 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.