The systems of sequences and the transition formulas, страница 2

          28.2 The combined method of an algorithm representation

            There are some cases algorithms are represented in the combined form. One branch of the algorithm may be represented in a form of the LSA, the others may be represented in a form of transition formulas or sequences.

            Using the transformation rules, it is possible to obtain homogeneous representation of the algorithm.

            Let it be, the algorithm is determined by the transition formulas and a sequence:

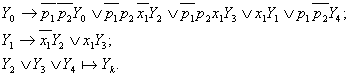                                 (28.4)

            Analysis of the representation shows, there are 4 operators Y₁, Y₂, Y₃, Y₄, the initial operator Y₀, the finishing operator Y_k.

            Having used the MSA completed respectively to (28.4), the next system of transition formulas is obtained:

           

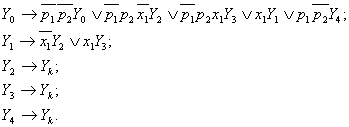
            If writing of formulas is performed along the columns of the MSA, the sequence system (28.3) is obtained.

28.3 Transforming of the transition formulas into the parenthetic form

            The transition formula in the form of (28.5) is called the reduction formula on the variable x_l.

,                                             (28.5)

            where x_lÎ{x₁,…,x_L}, A an B are the transition formulas inedependent on the x_l.

            An example of the reduction formula:

      (28.6)

            If a member of a transition formula doesn’t depend on the x_l, it is necessary to multiply this member by the expression  when reducing is performed. In this way, any transition formula may be reduced on any variable. For example, reducing the formula  (28.6) on the variable x₂ is following:

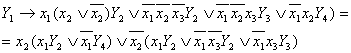        (28.7)