There are some ways of an algorithm representation:
1. The graphic scheme of an algorithm (the GSA) or a microprogram;
2. The matrix scheme of an algorithm (the MSA);
3. The logic scheme of an algorithm (the LSA);
4. The system of transition formulas;
5. The system of sequences;
6. The combined way.
Each of them has its own advantages and drawbacks.
In this lecture, the GSA, MSA and the system of transition formulas will be considered.
The graph scheme of an algorithm (the GSA) is an oriented connected graph containing one initial vertex Y0, one finishing vertex Yk, the set of conditional vertices X={x1, x2,…,xl}, the set of operational vertices Y={y1, y2,…, yl}. The initial vertex Y0 has a single output, no input (Fig.26.1a)). The finishing vertex Yk has a single input, no output (Fig.26.1b)). The operational vertex has a single input and a single output (Fig.26.1c)). The conditional vertex has a single input, two outputs (Fig.26.1d)). Sometimes, vertices of the GSA are called blocks.
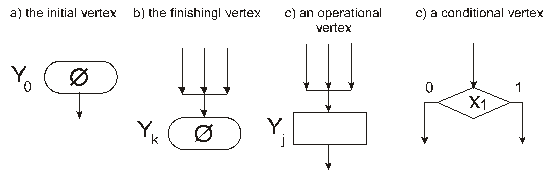
Figure 26.1 – The types of algorithm’s vertices
An example of the GSA is depicted in the Fig.26.2.
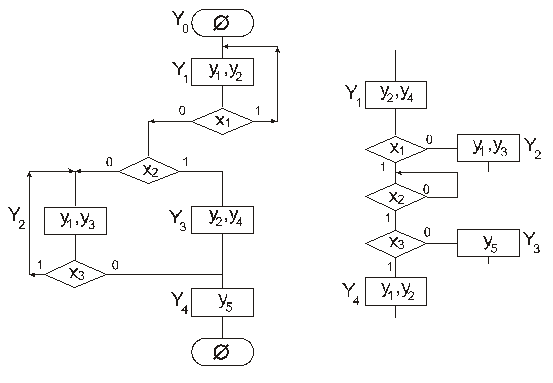
Figure 26.2 – An example of the GSA Figure
26.3 – A fragment of an algorithm with a recurrent vertex
The GSA is drawn respectively to the next rules and conditions:
1. The inputs and outputs of vertices are connected with edges between themselves, the edges are always oriented from an output to an input;
2. Each output is exactly connected to an input;
3. Each input is connected to at least one output;
4. For each vertex besides the initial and finishing, there is at least one path from the initial vertex to the finishing vertex, the vertex belongs to;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.