Преобразование структурных схем систем управления (Практическое занятие № 4)

Практическое занятие 4

Преобразование структурных схем систем управления

4.1. Теоретические положения

При исследовании систем автоматического регулирования их удобно представлять в виде структурных схем (блок-схем), на которых выделены отдельные динамические звенья с соответствующими передаточными функциями и связями между ними, которые показывают направление передачи сигналов. Как правило каждое звено имеет один входной и один выходной сигнал.

 Помимо звеньев на блок-схемах обозначаются также узлы (места разветвления сигналов) и сумматоры, объединяющие два и более входных сигналов в один выходной. Сумматор изображается в виде круга, разделенного на секторы, причем если входной сигнал инвертируется на входе сумматора, то соответствующий сектор заштриховывается. Знак минус может также быть написан рядом с соответствующим входом.

Пример блок-схемы приведен на рис.4.1.

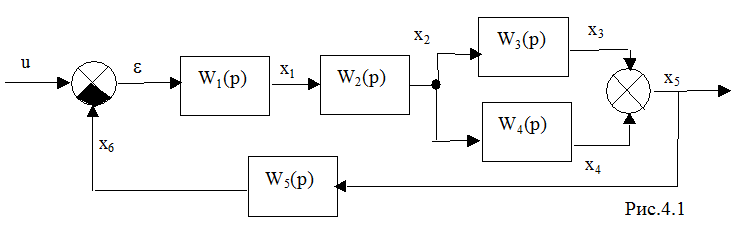
На данной схеме имеют место наиболее распространенные типы соединения динамических звеньев: последовательное, параллельное  и соединение с обратной связью.

Преобразование блок-схем линейных систем автоматического регулирования (преобразование передаточных функций) производится в соответствии с тремя основными правилами:

1)  Если звенья соединены последовательно, то результирующая передаточная функция  получается как произведение передаточных функций этих звеньев.

2)  Если звенья соединены параллельно, то результирующая передаточная функция  получается как сумма передаточных функций этих звеньев.

Это вытекает из принципа суперпозиции для линейных систем. В соответствии с первыми двумя правилами можно преобразовать блок-схему  (рис.4.1) к следующему виду (рис.4.2).

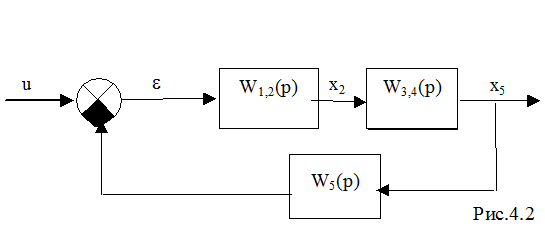
где W_1,2(p)=W₁(p) W₂(p).

    W_3,4(p)=W₃(p)+W₄(p).

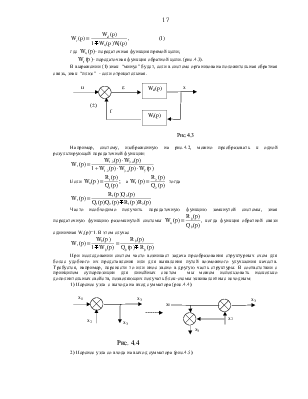
3)  Для соединения звеньев с обратной связью результирующая передаточная функция получится в виде

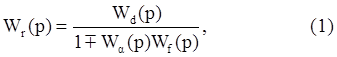
где - передаточная функция прямой цепи;

     - передаточная функция обратной цепи. (рис.4.3).

В выражении (1) знак  “минус” будет, если в системе организована положительная обратная связь, знак  “плюс”  - если отрицательная.

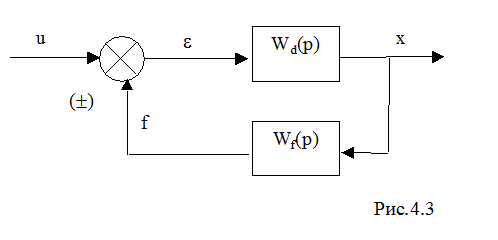
Например, систему, изображенную на рис.4.2, можно преобразовать к одной результирующей передаточной функции:

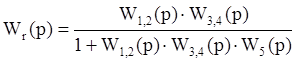
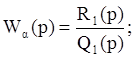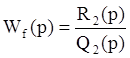Если    а   тогда

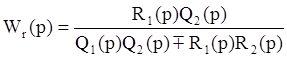
Часто необходимо получить передаточную функцию замкнутой системы, зная передаточную функцию разомкнутой системы 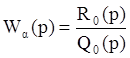, когда функция обратной связи единичная W_f(p)=1. В этом случае

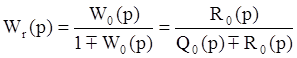
При исследовании систем часто возникает задача преобразования структурных схем для более удобного их представления или для выявления путей возможного улучшения качеств. Требуется, например, перенести то или иное звено в другую часть структуры. В соответствии с принципом суперпозиции для линейных систем  мы можем использовать несколько дополнительных свойств, позволяющих получать блок-схемы эквивалентные исходным:

1) Перенос узла  с выхода на вход сумматора (рис.4.4):

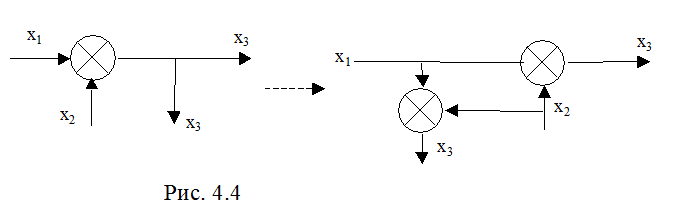
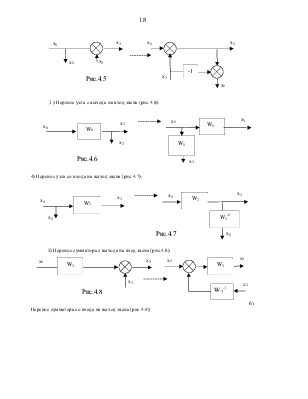
2) Перенос узла со входа на выход сумматора (рис.4.5):

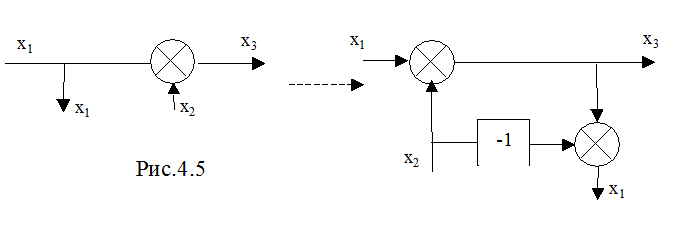
 3 ) Перенос узла с выхода на вход звена (рис.4.6):

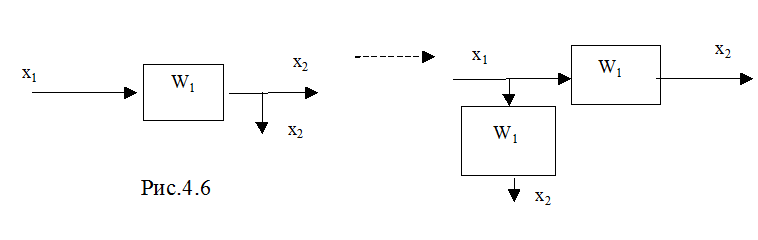4) Перенос узла со входа на выход звена (рис.4.7):

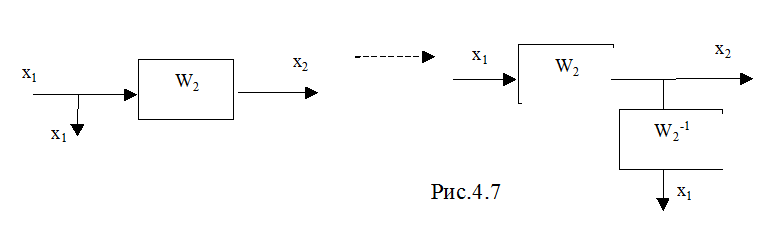
5) Перенос сумматора с выхода на вход звена (рис.4.8):

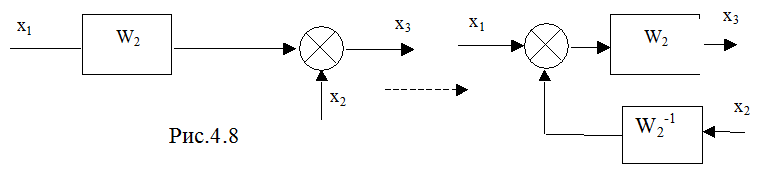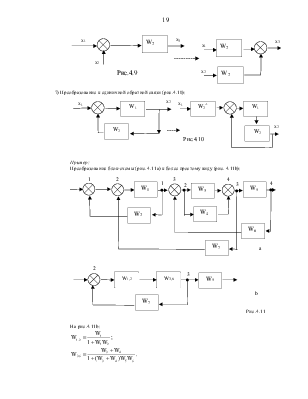
6) Перенос сумматора со входа на выход звена (рис.4.9):

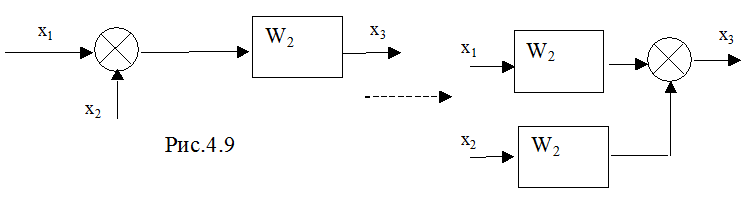 7) Преобразование к единичной обратной связи (рис.4.10):

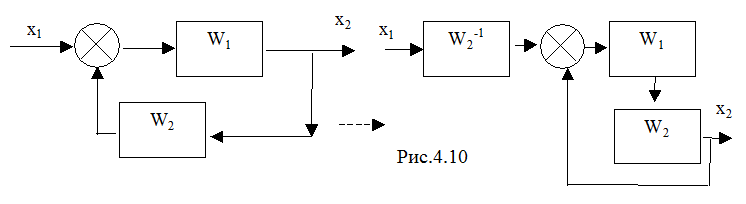
Пример:

Преобразование блок-схемы (рис. 4.11a) к более простому виду (рис. 4.11b):

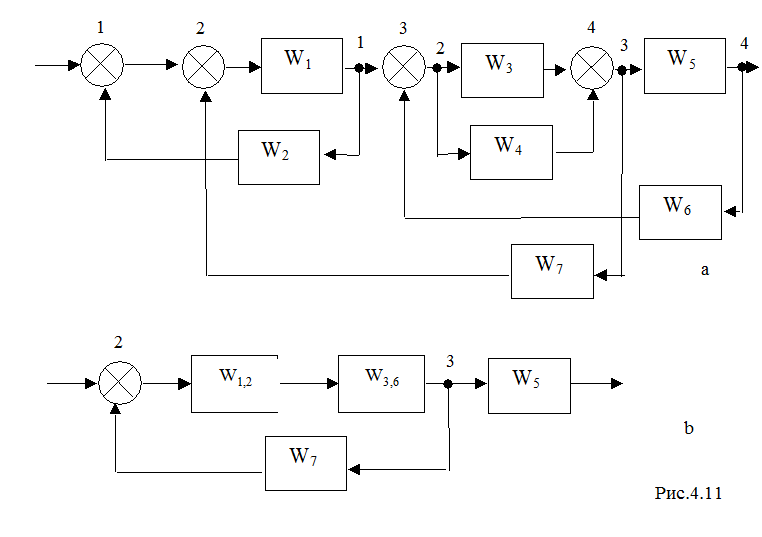
На рис.4.11b:

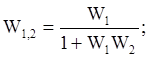
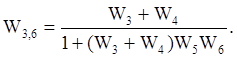
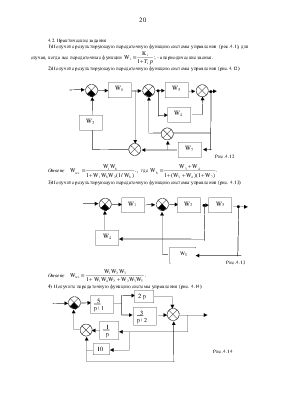
4.2. Практические задания

1) Получите результирующую передаточную функцию системы управления  (рис.4.1), для случая, когда все передаточные функции 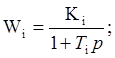 - апериодические звенья.

2) Получите результирующую передаточную функцию системы управления (рис.4.12)

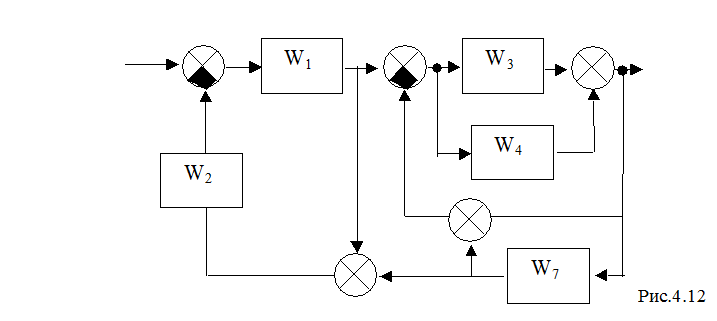
Ответ: 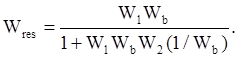  ,  где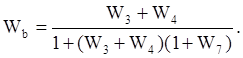

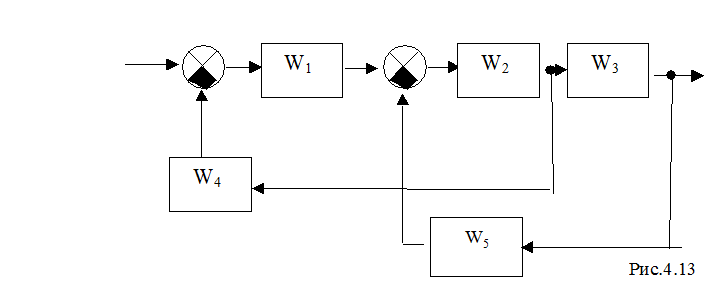
3) Получите результирующую передаточную функцию системы управления (рис. 4.13)

Ответ: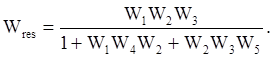    

4)  Получите передаточную функцию системы управления (рис. 4.14)

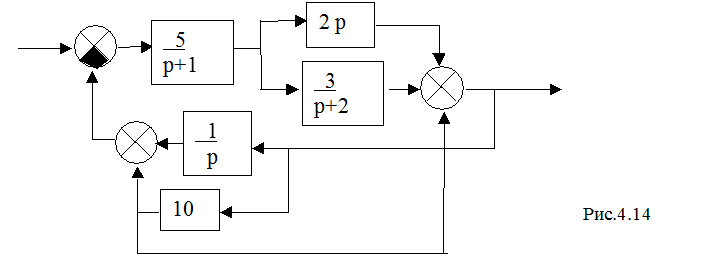
Ответ: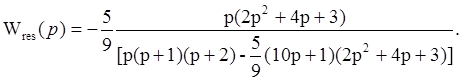    

4.3.   Контрольные вопросы

1)  Назовите основные правила построения и преобразования структурных схем.

2)  Из каких элементов состоят структурные схемы линейных систем автоматического регулирования?

3)  Чему равна результирующая передаточная функция последовательного соединения звеньев?

4)  Чему равна результирующая передаточная функция соединения звеньев с отрицательной обратной связью?

5)   Чему равна результирующая передаточная функция параллельного соединения звеньев?

6)  Как перенести сумматор со входа на выход динамического звена?

7)  Можно ли один сумматор разделить на два?

8)  Что называется узлом структурной схемы системы регулирования?

9)  Как перенести узел с выхода на вход динамического звена?

10)  Для чего используются преобразования структурных схем?