Лекция 13
Определение качества процессов в линейных динамических системах
План:
1. Понятие точности динамической системы, определение установившейся ошибки
2. Точность в гармоническом режиме
3. Коэффициенты ошибок
4. Анализ качества систем по переходным характеристикам
5. Анализ качества систем по частотным характеристикам
Качество систем регулирования прежде всего определяется их точностью. Под точностью автоматической системы понимают степень приближения выходной величины к ее заданному значению. Точность оценивается ошибкой х равной
x= g – xос
где g – заданное значение входной (регулируемой) величины
xос - действительное значение регулируемой величины в системе, представленной на рис. 1
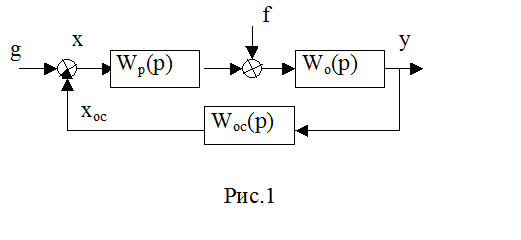
В случае отсутствия погрешностей в звеньях системы общая установившаяся статическая ошибка по теореме о конечном значении в преобразовании Лапласа определится по выражению
x = {Фx(p)G(p) + Фfx(p)F(p)}|p=0,
где Фx(p) и Фfx(p) – передаточные функции замкнутой системы по ошибке от управляющего и возмущающего воздействий соответственно;
G(p) и F(p) – изображения управляющего и возмущающего воздействий.
С точки зрения принципа суперпозиции возмущающее воздействие f(t) и управляющее воздействие g(t) действуют на линейную систему независимо, поэтому можно упрощенно рассматривать одно внешнее воздействие g(t) и одну передаточную функцию разомкнутой системы W(p)=Wp(p) Wo(p) Woc(p) приняв f(t)=0. Тогда изображение ошибки равно
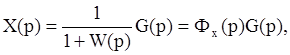
где 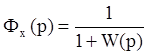 -
передаточная функция замкнутой системы по ошибке.
-
передаточная функция замкнутой системы по ошибке.
![]()
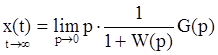
Пусть g(t)=1(t)·g0, где g0=const,
тогда 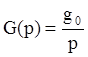 .
.
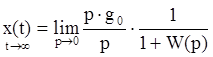
Если W(p) – передаточная функция статической системы ( ее числитель и знаменатель не имеют нулевых корней):
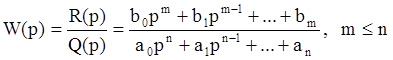 ,
,
то 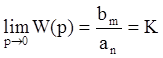 - есть общий
коэффициент передачи разомкнутой системы, называемый также добротностью.
- есть общий
коэффициент передачи разомкнутой системы, называемый также добротностью.
Таким образом 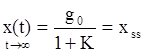 - установившаяся
ошибка при постоянном входном сигнале. Эта ошибка тем меньше, чем больше
добротность К. Для уменьшения ошибки вводят неединичную обратную связь, если
она не нарушает устойчивости системы.
- установившаяся
ошибка при постоянном входном сигнале. Эта ошибка тем меньше, чем больше
добротность К. Для уменьшения ошибки вводят неединичную обратную связь, если
она не нарушает устойчивости системы.
Если имеется передаточная функция астатической системы вида
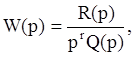
где r – порядок астатизма, тогда
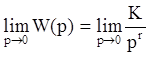 ,
,
тогда 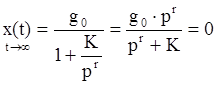 ,
,
То есть в астатической системе установившаяся ошибка
для постоянного входного воздействия равна нулю (![]() ).
).
Пусть теперь входной сигнал меняется по линейному закону:
![]()
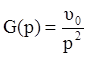
Для статической системы:
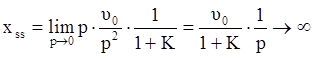 ,
,
то есть установившаяся ошибка неограниченно возрастает.
Для системы с астатизмом первого порядка:
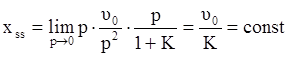 ,
,
т.e. величина установившейся ошибки пропорциональна скорости изменения входного сигнала и обратно пропорциональна коэффициенту передачи разомкнутой системы, который здесь будет называться добротностью по скорости.
Аналогично рассмотренному выше, предположим, что входное воздействие меняется с постоянным ускорением:
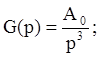
Для системы с астатизмом первого порядка установившаяся ошибка неограниченно возрастает во времени. Для системы с астатизмом второго порядка она будет постоянной:
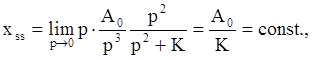
и для систем с более высоким порядком астатизма (r>2) эта ошибка стремится к нулю:
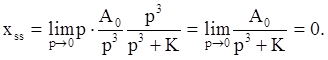
В следящих системах автоматического управления часто используется гармонический режим работы., при котором входное воздействие имеет вид:
![]() ,
,
где gm и ![]() -
постоянные или медленно меняющиеся амплитуда и частота сигнала.
-
постоянные или медленно меняющиеся амплитуда и частота сигнала.
В установившемся процессе в замкнутой системе также возникают гармонические колебания:
![]() ,
,
и точность системы можно оценить по амплитуде ошибки:
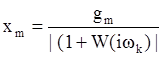
Если предположить, что xm<<gm , то
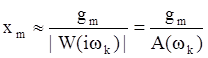 ,
,
где ![]() -значение
амплитудно–частотной характеристики на частоте
-значение
амплитудно–частотной характеристики на частоте ![]() .
.
Располагая логарифмической амплитудно–частотной
характеристикой легко оценить способность системы работать с установившейся
амплитудой ошибки, не превышающей заданную величину xm на частоте ![]() :
:
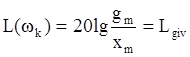 .,
.,
здесь Lgiv – заданное значение
логарифмической амплитудно–частотной характеристики [dB], которое называется
контрольной точкой. Если действительная логарифмическая АЧХ ![]() расположена выше, чем точка Lgiv
расположена выше, чем точка Lgiv
: ![]() ,
,
то система обеспечивает точность, заданную предельной амплитудой ошибки gm.
Если входное воздействие как функция времени имеет произвольную, но медленно меняющуюся форму, то ошибку автоматической системы можно определить следующим образом. Как известно, изображение ошибки замкнутой автоматической системы имеет вид
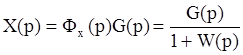
Разложим передаточную функцию ошибки в ряд по возрастающим степеням:
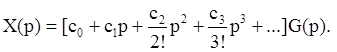 (1)
(1)
Этот
ряд сходится для малых значений ![]()
Переходя от изображения ошибки к ее оригиналу, получим формулу для вычисления ошибки для медленно меняющейся входной величины:
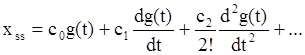
Коэффициенты c0, c1, c2…называются коэффициентами ошибок. Они показывают, какая часть от величины, ее скорости, ускорения и т.д. составляет ошибку. Коэффициенты ошибок могут определяться либо как соответствующие производные передаточной функции ошибки по переменной р при р=0
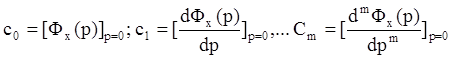 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.