Определение качества процессов в линейных динамических системах, страница 2

либо простым делением числителя на знаменатель передаточной функции ошибки, так как она представляет собой рациональную дробь.

Например, если передаточную функцию представить в виде

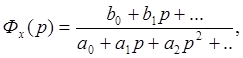
то коэффициенты ошибок определяются так

.

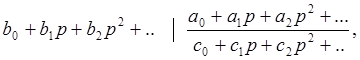Коэффициент c₀≠0 только для статических систем. Для систем с астатизмом первого порядка  c₀=0; 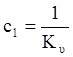; для систем с астатизмом второго порядка c₀=0; c₁=1; 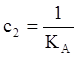 и т.д.

Пример:

Пусть передаточная функция разомкнутой системы имеет вид:

 .

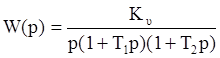Передаточная функция замкнутой системы по ошибке:

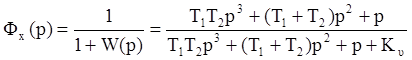
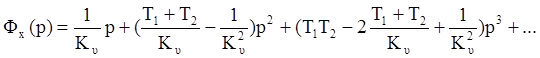
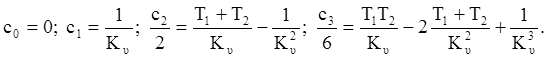
Если управляющее воздействие будет иметь вид:

,

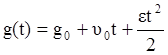то установившаяся ошибка будет определяться формулой:

.

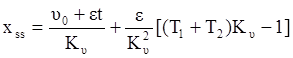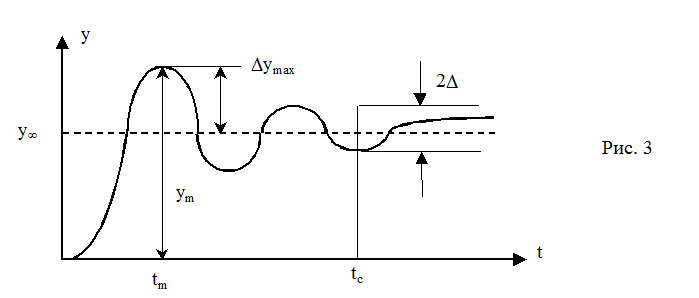
Качество процесса  управления в системе можно оценить, используя переходную характеристику. Как известно,  основными параметрами этой характеристики являются величина перерегулирования  и время регулирования (t_c)  (рис. 2)

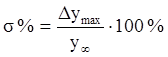
Допустимая величина σ определяется  индивидуально для каждой системы в соответствии с ее назначением и условиями функционирования. Обычно полагают в качестве хорошего значения величину σ =10..30%.

Быстродействие системы можно оценить по величине времени t_c. Переходный процесс считается законченным, если выходная величина системы удовлетворяет условию

где Δ  - заданное малое значение установившейся ошибки. В соответствии с приведенными двумя параметрами, переходный процесс можно считать качественным, если он лежит внутри разрешенной зоны (рис. 3а).

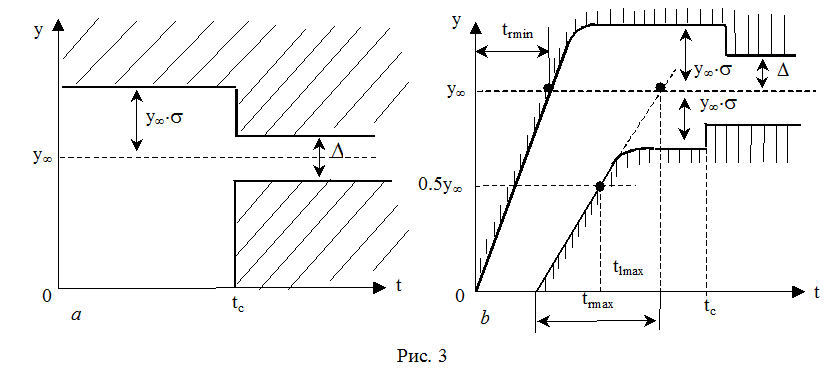
Дальнейшее развитие данных критериев качества ведет к  появлению дополнительных ограничений на следующие величины:

1)  время нарастания (t_r) – время между  пересечением оси времени и касательной к осредненной кривой переходного процесса  и  пересечением  прямой линии y_∞ и указанной  касательной переходного процесса

2)  время запаздывания(t_L)   - время между моментом приложения скачкообразного воздействия  и достижением осредненной величиной выходной координаты половины установившегося значения y_∞.

В соответствии с заданными величинами t_rmin, t_rmax, t_Lmax допустимая область расположения переходной характеристики  приобретает более сложную форму (рис.3b).

Зная вид переходной характеристики, иногда более полезно применить интегральную оценку качества процесса регулирования. Простейший вид такой оценки – это интеграл ошибки в переходном процессе (рис. 4а)

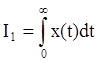
Величина  I₁ конечна, если .

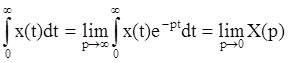
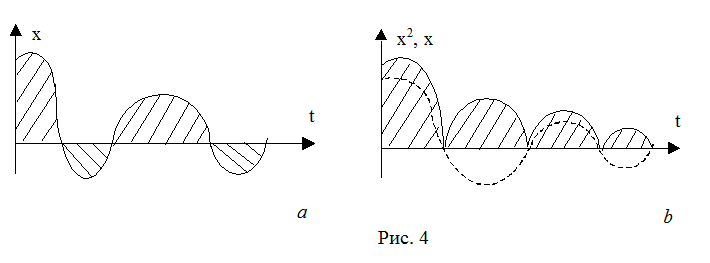
Величина  I₁ не очень удобна для колебательных процессов, так как положительные и отрицательные полуволны взаимно уничтожаются в ней. Поэтому применяют другие виды интегральных оценок. (рис.4b).

;

.

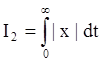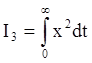Во всех случаях для улучшения качества переходного процесса  следует минимизировать  величину интегральной оценки.

Для того,  чтобы использовать критерий качества, связанный  с переходной характеристикой системы, необходимо получить эту характеристику. Сейчас для этого обычно используют численные методы моделирования  линейных или нелинейных систем на компьютерах. Однако эти вычисления  часто требуют больших затрат времени,  и для более быстрой оценки качества используют частотные критерии и оценки. Из них наиболее часто используют величины запасов устойчивости по амплитуде и по фазе, так как с  ними тесно связана величина перерегулирования.

Для амплитудно-фазовой характеристики системы (рис.5) можно указать запас устойчивости  по фазе   и два запаса устойчивости по амплитуде.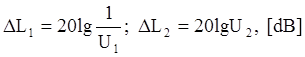

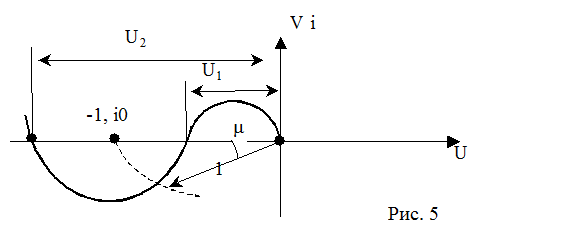
В хорошо демпфированной системе обычно соблюдаются условия

Для абсолютно устойчивой системы

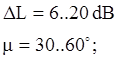
Более удобно оценивать качество системы не по двум DL и Dm  , а по одному параметру , который называют  показателем колебательности. Его величин равна максимальному значению амплитуды частотной характеристики..

Если входной сигнал гармонический, то в линейной системе и выходной сигнал также имеет гармонический характер, и тогда

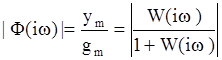
Показатель колебательности равен: 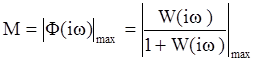(2)

Для хорошо демпфированной системы M=1,1….1,5, но иногда допускаются и величины .

В соответствии с выражением (2) можно записать:

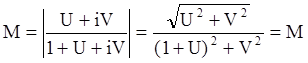
(3)

где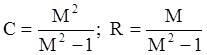

Выражение (3) представляет собой уравнение окружности с радиусом R и центром, смещенным из начала координат на величину С вдоль действительной оси. Для того, чтобы получить замкнутую систему с показателем колебательности , необходимо, чтобы частотная характеристика  разомкнутой системы W(iω). располагалась бы вне  окружности, определенной для данного  (рис. 6).

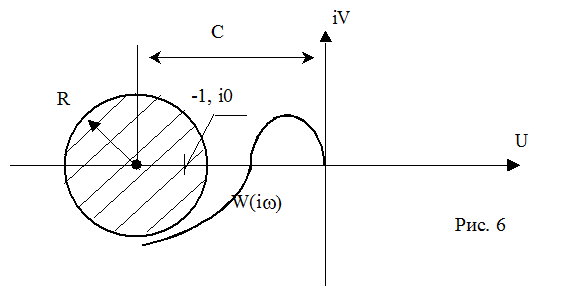
Указанная окружность фвляется запрещенной зоной для характеристики W(iω). Таким же образом можно получить и запрещенную зону для логариямической фазочастотной характеристики (рис. 7).

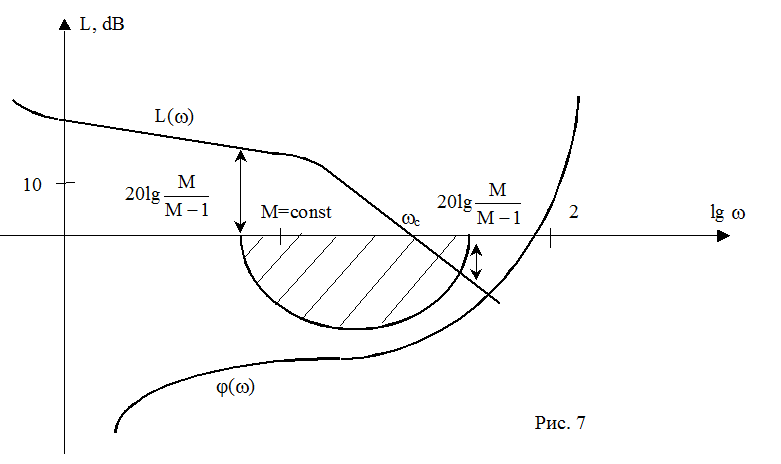
Для определения быстродействия системы по частотной характеристике можно применить оценку по следующим величинам: 1)  - – частота среза (там, где A()=1); 2) - - частота пропускания: определяется  для A()=0,707 (-3dB) (важна для замкнутой системы). Эти показатели определяются в соответствии с индивидуальными требованиями к системе. Они показывают способность системы отрабатывать сигналы в заданном диапазоне частот.