Передаточные функции систем управления. Связь между передаточной и весовой функциями

Лекция 8

Передаточные функции систем управления

План

1. Передаточная функция системы

2. Связь между передаточной и весовой функциями

3. Одностороннее преобразование Фурье. Частотная передаточная функция

4. Передаточная функция импульсной системы

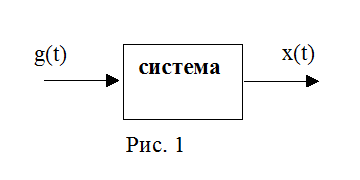
Передаточной функцией системы или звена называется отношение изображений по Лапласу выходного и входного сигналов при нулевых начальных условиях  (рис. 1).

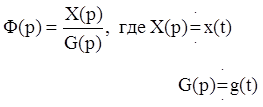
Напомним соотношение из предыдущей лекции:

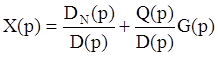
Если D_N(p)º0 то

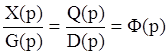
Q(p) и D(p) полиномы,  вид которых зависит только от системы и не зависят от изображений сигналов по Лапласу.

Пример: Пусть имеем дифференциальное уравнение системы:

В соответствии с принципом суперпозиции можно записать:

x=x₁+x₂,  тогда

 

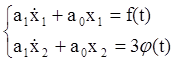
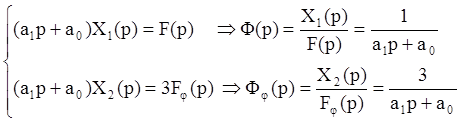
Из примера видно, что для каждого из входов системы мы получаем свою передаточную функцию Если дифференциальное уравнение имеет вид:

D(p)x(t)=Q(p)g(t)+N(p)f(t),

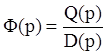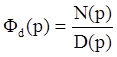то  будем называть передаточной функцией по управлению и  будем называть передаточной функцией по возмущению.

Передаточная функция системы или звена связана с весовой (импульсной переходной) характеристикой через преобразование Лапласа:

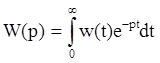
Докажем это на примере:

Как известно, w(t)  - это реакция системы на воздействие d(t) . Пусть имеем дифференциальной уравнение системы

 

В изображении по Лапласу:

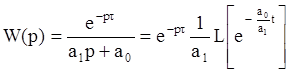
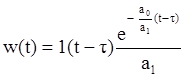
В то же время w(t)=h’(t). Можно легко показать, что 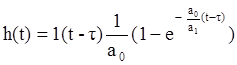 и  .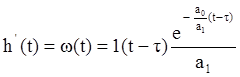

Если в передаточной функции заменить  p на jw , то получим частотную передаточную функцию, связывающую изображения выходного и входного сигналов в преобразовании Фурье:

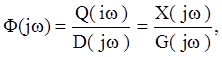
где 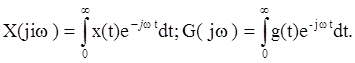- одностороннее преобразование Фурье сигнала.

Частотная передаточная функция линейной системы показывает связь между входным и выходным гармоническими сигналами:

Пусть входной сигнал имеет вид:

а выходной:

Используя формулу Эйлера, можно записать:

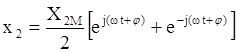
Поскольку две компоненты этой функции антисимметричны,  то

Найдем связь между амплитудой и фазой этих сигналов:

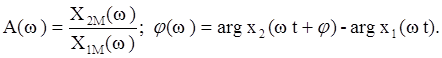
Когда мы применяем к  W (р) преобразование Фурье,  то получаем соотношение:

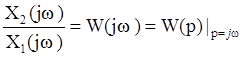
Частотную передаточную функцию можно представить в виде суммы действительной и мнимой частей  или как годограф, описываемый вектор, амплитуда которого выражается амплитудно-частотной  характеристикой, а фаза - фазочастотной:

,

где ;

.

На комплексной плоскости этот годограф имеет  симметричный вид, представленный на рис.2

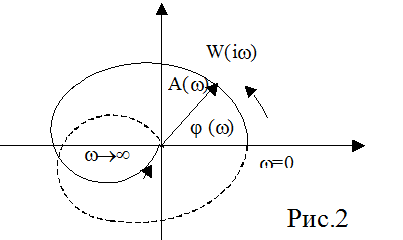
Частотная передаточная функция является изображением по Фурье от весовой функции системы:

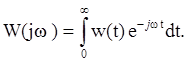
Для дискретных систем вводится импульсная передаточная функция. Она связывает Z-преобразования выходного и входного сигналов системы.

Аналогично непрерывным системам  Z-передаточная функция является для импульсной системы Z-преобразованием импульсной (решетчатой) весовой функции:

Если x₁[n] – входной дискретный сигнал  и x₂[n] – выходной дискретный сигнал,  то

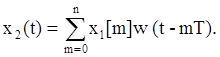
Для дискретных моментов времени:

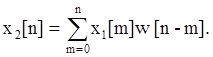
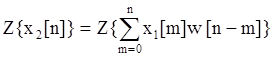
В соответствии с теоремой свертки: