




Республика Беларусь
Кафедра «Высшая математика»
Типовой расчёт
по разделу высшей математики
«Ряды Фурье»
Проверил:
преподаватель
Дудко С.А.
Выполнил:
студент группы ЭТ-21
Семеняко К.С.
Гомель 2012
1. Дана
функция ![]() в интервале
в интервале ![]() .
Разложить эту функцию:
.
Разложить эту функцию:
а) в ряд Фурье по синусам;
б) в ряд Фурье по косинусам.
1)
![]() ;
; ![]() .
.
2)
![]() ;
; ![]() .
.
3)
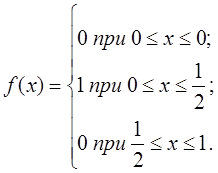
![]() .
.
4)
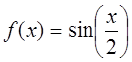 ;
; ![]() .
.
Решение.
1) ![]() ;
; ![]() .
.
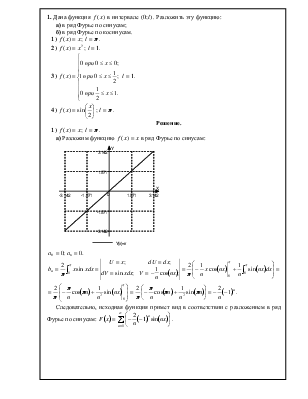
а) Разложим
функцию ![]() в ряд Фурье по синусам:
в ряд Фурье по синусам:
![]()
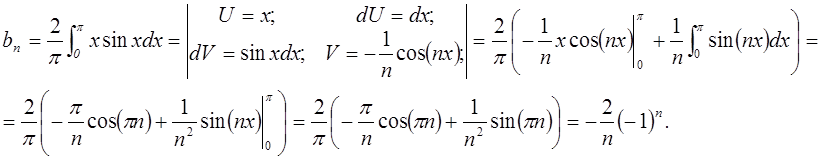
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по синусам: 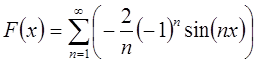 .
.
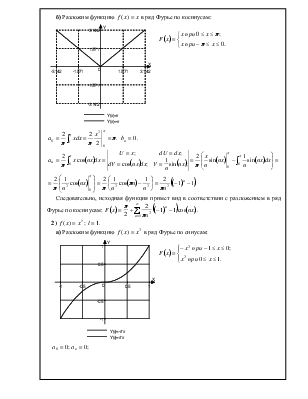
б) Разложим
функцию ![]() в ряд Фурье по косинусам:
в ряд Фурье по косинусам:
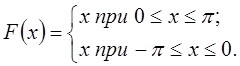
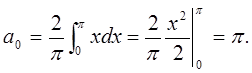
![]() .
.
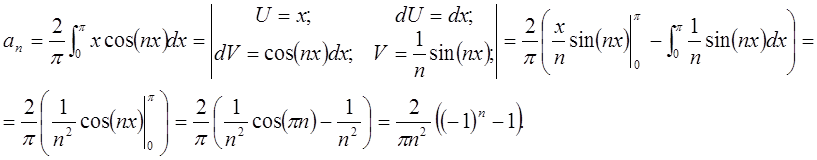
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по косинусам: 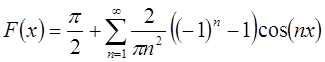 .
.
2) ![]() ;
; ![]() .
.
а) Разложим
функцию ![]() в ряд Фурье по синусам:
в ряд Фурье по синусам:
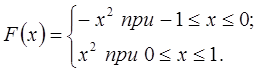
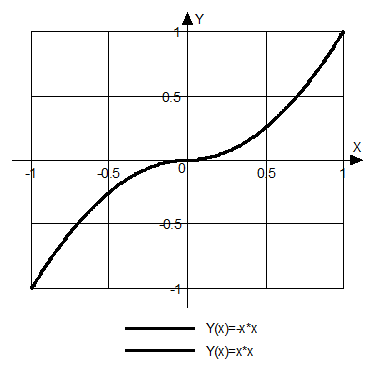
![]()
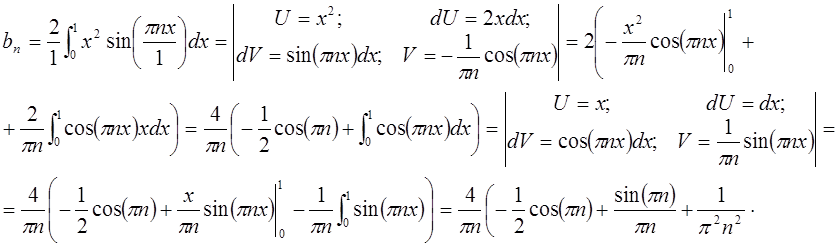
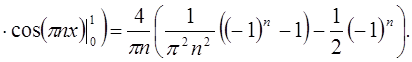
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по синусам: 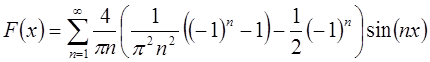 .
.
б) Разложим
функцию ![]() в ряд Фурье по косинусам:
в ряд Фурье по косинусам:
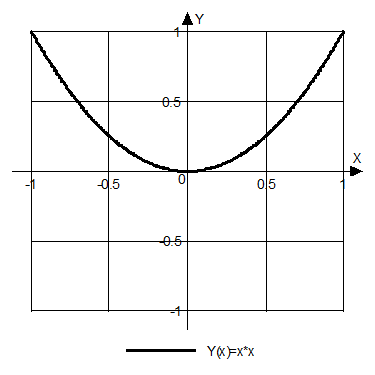
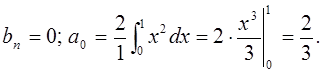
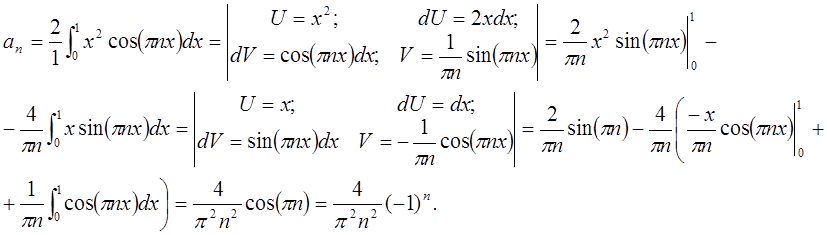
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по косинусам: 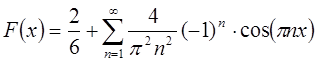 .
.
3)
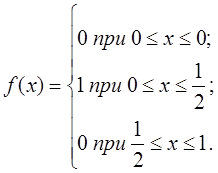
![]() .
.
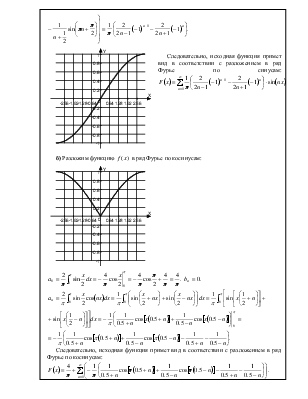
а) Разложим
функцию ![]() в ряд Фурье по синусам:
в ряд Фурье по синусам:
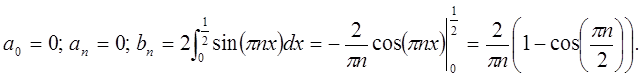
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по синусам: 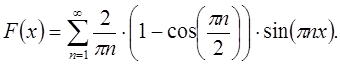
б) Разложим
функцию ![]() в ряд Фурье по косинусам:
в ряд Фурье по косинусам:
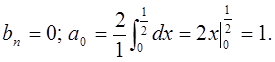
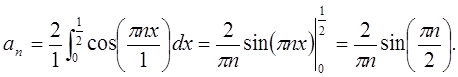
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по косинусам: 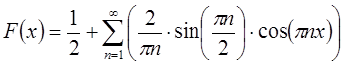 .
.
4)
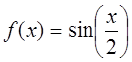 ;
; ![]() .
.
а) Разложим
функцию ![]() в ряд Фурье по синусам:
в ряд Фурье по синусам:
![]() .
. 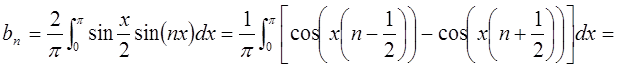
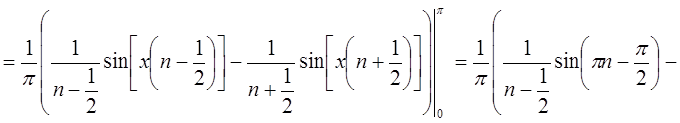
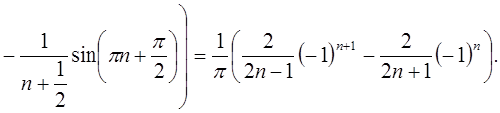
Следовательно, исходная функция примет вид в
соответствии с разложением в ряд Фурье по синусам: 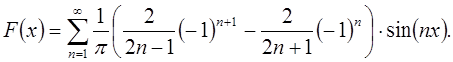
б) Разложим
функцию ![]() в ряд Фурье по косинусам:
в ряд Фурье по косинусам:
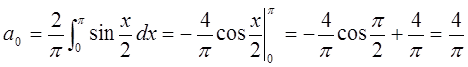 .
. ![]() .
.
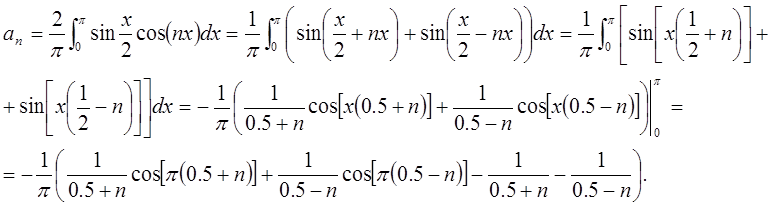
Следовательно, исходная функция примет вид в соответствии с разложением в ряд Фурье по косинусам:
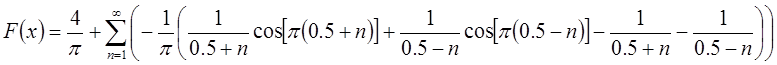 .
.
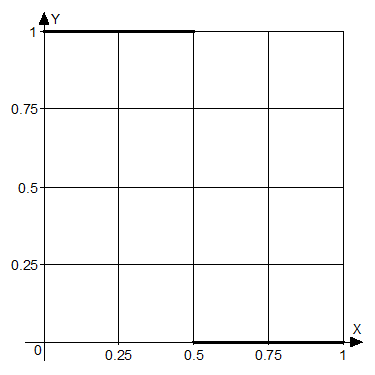
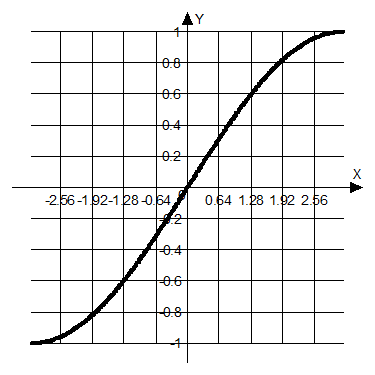
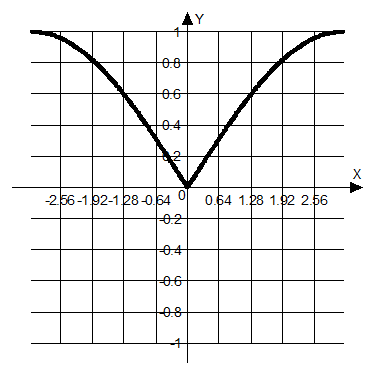
2. Разложить
в ряд Фурье функцию ![]() , изображённую на рисунке.
, изображённую на рисунке.
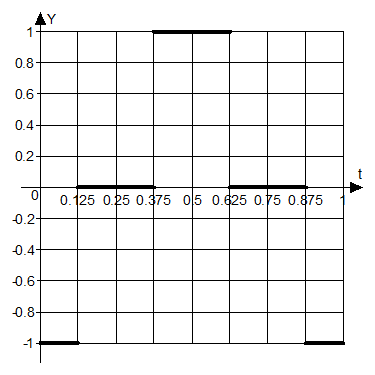
(на
данном графике период ![]() взят равным единице, а
взят равным единице, а ![]() - тоже единице).
- тоже единице).
Решение.
Запишем эту функцию:
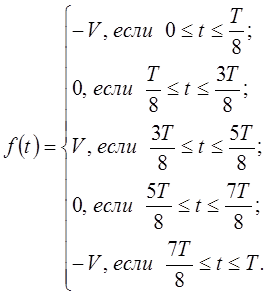 Разложим её в ряд Фурье:
Разложим её в ряд Фурье:
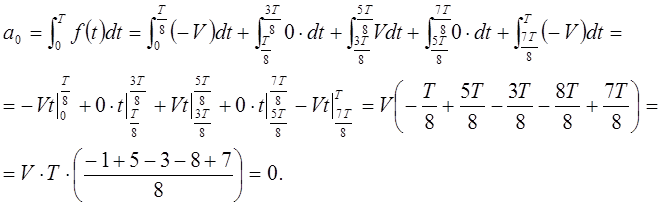
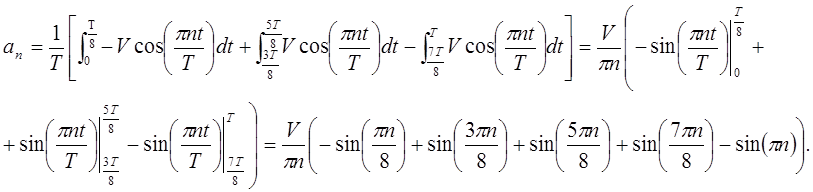
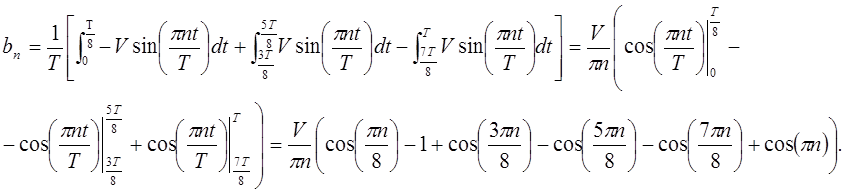
Следовательно, исходная функция примет вид в соответствии с разложением в ряд Фурье:
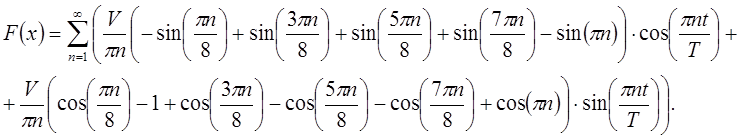 .
.
3. Представить тригонометрическим многочленом третьего
порядка функцию ![]() , заданную таблицей:
, заданную таблицей:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
36 |
50 |
40 |
30 |
10 |
20 |
30 |
50 |
40 |
30 |
Решение:
Далее приводится листинг программы на языке C/C++:
#include <stdio.h>
#include <math.h>
#include <iostream.h>
const float y[]={0,10,20,30,36,50,40,30,10,20,30,50,40,30};
void main(void)
{
float a[13],b[13],x[13],g[13],s,q,c;
for (int i=1;i<=13;i++)
{
x[i]=s;s=s+M_PI/6;
}
for (i=1;i<=12;i++) q=q+y[i];
q=q/6;
for (int k=1;k<=4;k++)
{
s=0;c=0;
for (int i=1;i<=12;i++)
{
s=s+y[i]*cos(k*x[i]);
c=c+y[i]*sin(k*x[i]);
}
a[k]=s/6; b[k]=c/6;
}
cout<<"x[i] y[i] g[i]\n";
for (i=1;i<=13;i++)
{g[i]=q/2;
for (int k=1;k<=4;k++) g[i]=g[i]+a[k]*cos(k*x[i])+b[k]*sin(k*x[i]);
printf("%.3f %.0f %.3f\n",x[i],y[i],g[i]);}
}
Результат выполнения программы:
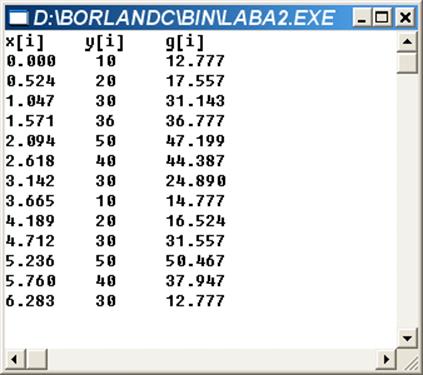
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.